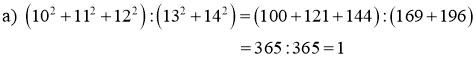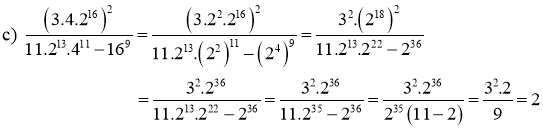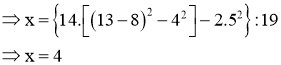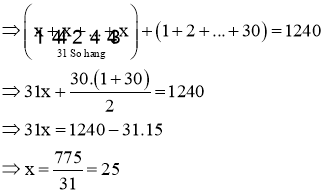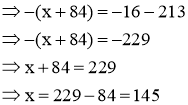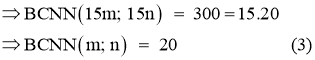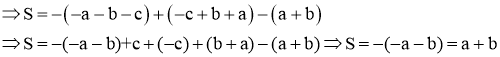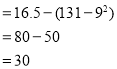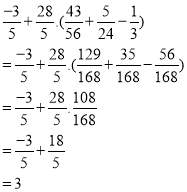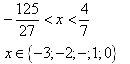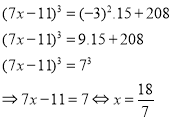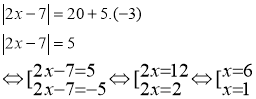ĐỀ 1
Câu 1. ( 2,0 điểm)
Cho A = 2 + 22 + 23 + 24 + . . . + 220. Tìm chữ số tận cùng của A.
Câu 2. ( 1,0 điểm)
Số tự nhiên n có 54 ước. Chứng minh rằng tích các ước của n bằng n27.
Câu 3. ( 1,5 điểm)
Chứng minh rằng: n( n +1)( 2n +1)( 3n + 1)( 4n +1) chia hết cho 5 với mọi số tự nhiên n.
Câu 4. ( 1,0 điểm)
Tìm tất cả các số nguyên tố p và q sao cho các số 7p + q và pq + 11 cũng là các số nguyên tố.
Câu 5. ( 1,5 điểm)
a) Tìm ƯCLN( 7n +3, 8n - 1) với (n €N*). Tìm điều kiện của n để hai số đó nguyên tố cùng nhau.
b) Tìm hai số tự nhiên biết: Hiệu của chúng bằng 84, ƯCLN của chúng bằng 28 và các số đó trong khoảng từ 300 đến 440.
Câu 6. ( 1,0 điểm)
Tìm các số nguyên x, y sao cho: xy – 2x - y = -6.
Câu 7. ( 2,0 điểm)
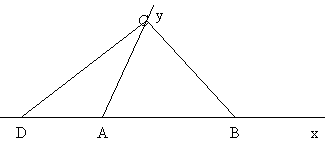
Cho xAy, trên tia Ax lấy điểm B sao cho AB = 5 cm. Trên tia đối của tia Ax lấy điểm D sao cho AD = 3 cm, C là một điểm trên tia Ay.
a. Tính BD.
b. Biết ![]() .
.
c. Biết AK = 1 cm (K thuộc BD). Tính BK.
Đáp án đề thi học sinh giỏi môn Toán lớp 6
Câu | Đáp án | Điểm |
Câu 1 (2,0 điểm) | A. 2 = (2 + 22 + 23 + 24 + . . . + 220.). 2 = 22 + 23 + 24 + 25 + . . . + 221. Nên A.2 - A = 221 -2 A = 221 - 2 |
0,5 0,5 |
Ta có : 221 = 24.5+1 = (24)5 . 2 = 165 .2 ... 165 có tận cùng là 6 . Nên 165 . 2 có tận cùng là 6. 2 có tận cùng là 2. Vậy A có tận cùng là 2. |
0,5 0,5 | |
Câu 2. (1,0 điểm)
| Số tự nhiên n có 54 ước. Chứng minh rằng tích các ước của n bằng n27.
|
0,25
0,25
0,25
0,25 |
Câu 3 (1,5 điểm) | Với mọi số tự nhiên n ta có các trường hợp sau: TH1: n chia hết cho 5 thì tích chia hết cho 5. TH 2: n chia cho 5 dư 1 thì n = 5k +1 4n +1= 20k + 5 chia hết cho 5 tích chia hết cho 5. TH3: n chia cho 5 dư 2 thì n = 5k +2 2n +1= 10k + 5 chia hết cho 5 tích chia hết cho 5. TH4: n chia cho 5 dư 3 thì n = 5k +3 3n +1= 15k + 10 chia hết cho 5 tích chia hết cho 5. TH 5: n chia cho 5 dư 4 thì n = 5k +4 n +1= 5k + 5 chia hết cho 5 tích chia hết cho 5. Vậy : n( n +1)( 2n +1)( 3n + 1)( 4n +1) chia hết cho 5 với mọi số tự nhiên n. |
0,25
0,25
0,25
0,25
0,25
0,25 |
Câu 4 (1,0 điểm) | Nếu pq + 11 là số nguyên tố thì nó phải là số nguyên tố lẻ ( vì pq + 11 > 2) pq là số chẵn ít nhất 1 trong 2 số phải chẵn, tức là bằng 2. + Giả sử p = 2. Khi đó 7p + q = 14 + q ; pq + 11 = 2q + 11. Thử q = 2( loại) q = 3( t/m) q > 3 có 1 số là hợp số. p = 2 và q = 3. + Giả sử q = 2. Giải TT như trên ta được p = 3. Vậy p = 2; q = 3 hoặc p = 3; q = 2. |
0,25
0,25
0,25
0,25 |
Câu 5 (1,5 điểm) | a) Gọi ƯCLN( 7n +3, 8n - 1) = d với (n €N*) Ta có: 7n +3 8.( 7n +3) – 7.( 8n - 1) Để hai số đó nguyên tố cùng nhau thì d ≠ 31. Mà 7n + 3 n – 4 n = 31k + 4( với k là số tự nhiên) Do đó d ≠ 31 n ≠ 31k + 4. Vậy hai số 7n +3, 8n – 1 nguyên tố cùng nhau khi n ≠ 31k + 4( với k là số tự nhiên). b) Gọi hai số phải tìm là a và b ( a, b N* , a > b) Ta có: ƯCLN(a, b) = 28 nên a = 28k và b = 28q . Trong đó k, qN*và k, q nguyên tố cùng nhau. Ta có : a - b = 84 k - q = 3 Theo bài ra: 300 ≤ b < a ≤ 440 10 < q < k <16. Chọn hai số có hiệu bằng 3 trong khoảng từ 11 đến 15 là 11 và 14; 12 và 15. Chỉ có 11 và 14 là hai số nguyên tố cùng nhau. nên q = 11và k = 14. Ta có : a = 28. 11 = 308 ; b = 28. 14 = 392 Vậy hai số phải tìm là 308 và 392. |
0,25
0,25 0,25
0,25
0,25
0,25 |
Câu 6 (1,0 điểm) | xy – 2x - y = -6 (x – 1)( y - 2) = -4. Với x, y là số nguyên, ta có bảng: x - 1-11-22-44 y - 24-42-21-1 x02-13-35 y6-24031 Vậy các số x, y thỏa mãn là: ( x,y) {( 0;6); (2;-2); (-1;4)…}
| 0,5
0,5 |
Câu 7 (2,0 điểm)
|
a) Tính BD Vì B thuộc tia Ax, D thuộc tia đối của tia Ax
b) Biết BCD = 850, BCA = 500. Tính ACD
=> ACD = BCD - ACB = 850 - 500 = 350 c) Biết AK = 1 cm (K thuộc BD). Tính BK * Trường hợp 1: K thuộc tia Ax - Lập luận chỉ ra được K nằm giữa A và B - Suy ra: AK + KB = AB
* Trường hợp 2: K thuộc tia đối của tia Ax - Lập luận chỉ ra được A nằm giữa K và B - Suy ra: KB = KA + AB
* Kết luận: Vậy KB = 4 cm hoặc KB = 6 cm | 0,25
0,25
0,5
0, 5
0, 5 |
ĐỀ 2
Bài 1: (1,0điểm) Thực hiện phép tính (tính hợp lý nếu có thể)
a/ 1968: 16 + 5136: 16 -704: 16
b/ 23. 53 - 3 {400 -[ 673 - 23. (78: 76 +70)]}
Bài 2: (1,0điểm) M có là một số chính phương không nếu:
M = 1 + 3 + 5 +…+ (2n-1) (Với n ![]() N , n
N , n ![]() 0)
0)
Bài 3: (1,5điểm) Chứng tỏ rằng:
a/ (3100+19990) ![]() 2
2
b / Tổng của 4 số tự nhiên liên tiếp không chia hết cho 4
Bài 4: (1,0điểm) So sánh A và B biết:
A = ![]() , B =
, B = ![]()
Bài 5: (2,0điểm) Tím tất cả các số nguyên n để:
a) Phân số ![]() có giá trị là một số nguyên
có giá trị là một số nguyên
b) Phân số ![]() là phân số tối giản
là phân số tối giản
Bài 6: (2,5điểm)
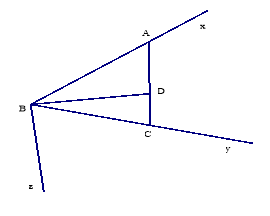
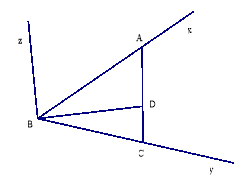
Cho góc xBy = 550.Trên các tia Bx, By lần lượt lấy các điểm A, C (A ![]() B, C
B, C![]() B). Trên đoạn thẳng AC lấy điểm D sao cho góc ABD = 300
B). Trên đoạn thẳng AC lấy điểm D sao cho góc ABD = 300
a/ Tính độ dài AC, biết AD = 4cm, CD = 3cm
b/ Tính số đo góc DBC
c/ Từ B vẽ tia Bz sao cho góc DBz = 900. Tính số đo ABz.
Bài 7: (1,0điểm) Tìm các cặp số tự nhiên x , y sao cho: (2x + 1)(y – 5) = 12
---------- HẾT ----------
(Đề thi gồm có 01 trang).
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:.......................................; Số báodanh.........................
| HƯỚNG DẪN CHẤM Môn thi: Toán - Lớp 6
|
![]() Bài 1: (1,0 điểm)
Bài 1: (1,0 điểm)
Ý/Phần | Đáp án | Điểm |
a | = 16(123+ 321 - 44):16 | 0,25 |
| = 400 | 0,25 |
b | =8.125-3.{400-[673-8.50]} | 0,25 |
| = 1000-3.{400-273} =619 |
0,25 |
![]()
Bài 2: (1,0 điểm)
Ý/Phần | Đáp án | Điểm |
| M = 1 + 3 + 5 +…+ (2n-1) (Với n Tính số số hạng = (2n-1-1): 2 + 1 = n | 0,5
|
| Tính tổng = (2n-1+1) n: 2 = 2n2: 2 = n 2 KL: M là số chính phương | 0,5đ |
Bài 3: (1,5 điểm)
Ý/Phần | Đáp án | Điểm |
a | Ta có: 3100 = 3.3.3….3 (có 100 thừa số 3) = (34)25 = 8125 có chữ số tận cùng bằng 1 19990 = 19.19…19 (có 990 thứa số 19) = (192)495 = 361495 (có chữ số tận cùng bằng 1 Vậy 3100+19990 có chữ số tận cùng bằng 2 nên tổng này chia hết cho 2 |
0,25
0,25
0,5 |
b | Gọi 4 số tự nhiên liên tiếp là: a; (a +1);(a + 2);(a + 3); (a Ta có: a + (a+1) + (a+2) + (a+3) = 4a + 6 Vì 4a | 0,25
0,25 |
Bài 4: (1,0 điểm)
Ý/Phần | Đáp án | Điểm |
| Vì A = Vậy A < B | 0,75
0,25 |
Bài 5: (2,0 điểm)
Ý/Phần | Đáp án | Điểm |
a
| Ta có (n+1) = Vậy (n+1) (n-2) => n
| 0.5
0,5 |
b | Gọi d là ƯC của 12n+1 và 30n+2 (d | 0,25 |
| 0,5đ | |
Vậy phân số đã cho tối giản | 0,25 |
Bài 6: (2,5 điểm)
Ý/Phần | Đáp án | Điểm |
a
b
| Vẽ hình đúng TH1 TH2
Vì D thuộc đoạn thẳng AC nên D nằm giữa A và C: AC= AD + CD = 4+3 = 7 cm Chứng minh được tia BD nằm giữa hai tia BA và BC Ta có đẳng thức: =550 – 300 = 250
|
0,25
0,25 0,25 0,25
0,5 |
c | Xét hai trường hợp: - Trường hợp 1: Tia Bz và tia BD nằm về hai phía nửa mặt phẳng có bờ là AB nên tia BA nằm giữa hai tiaBz và BD Tính được - Trường hợp 2:Tia Bz và tia BD nằm về cùng nửa mặt phẳng có bờ là AB nên tia BD nằm giữa hai tia Bz và BA Tính được |
0,25
0,25 0,25
0,25 |
![]() Bài 7: (1,0 điểm)
Bài 7: (1,0 điểm)
Ý/Phần | Đáp án | Điểm |
| (2x+ 1); (y - 5) là các ước của 12 | 0,25 |
| Ư(12) = | 0,25 |
| Vì 2x + 1 là lẻ nên: 2x + 1= 1 2x + 1= 3 Vậy với x = 0 thì y = 17; Với x = 1 thì y = 9 |
0,25 0,25 |
ĐỀ SỐ 3
Bài 1 : (5 điểm) Thực hiện các phép tính sau một cách hợp lý :
a) ![]() .
.
b) ![]()
c) 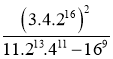
d) 1152 - (374 + 1152) + (-65 + 374)
e) 13 - 12 + 11 + 10 - 9 + 8 - 7 - 6 + 5 - 4 + 3 + 2 - 1
Bài 2 : (4 điểm) Tìm x, biết:
a) ![]()
b) ![]()
c) 11 - (-53 + x) = 97
d) -(x + 84) + 213 = -16
Bài 3 : (2 điểm) Tìm hai số tự nhiên a và b, biết: BCNN(a,b)=300; ƯCLN(a,b)=15 và a+15=b.
Bài 4 : (3 điểm)
a) Tìm số nguyên x và y, biết : xy - x + 2y = 3.
b) So sánh M và N biết rằng : 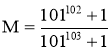 .
.
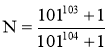 .
.
Bài 5 : (6 điểm) Cho đoạn thẳng AB, điểm O thuộc tia đối của tia AB. Gọi M, N thứ tự là trung điểm của OA, OB.
a) Chứng tỏ rằng OA < OB.
b) Trong ba điểm O, M, N điểm nào nằm giữa hai điểm còn lại ?
c) Chứng tỏ rằng độ dài đoạn thẳng MN không phụ thuộc vào vị trí của điểm O (O thuộc tia đối của tia AB).
![]()
B - PHẦN ĐÁP ÁN :
Bài 1 : (5 điểm) Thực hiện các phép tính sau một cách hợp lý :
Đáp án | Điểm |
| 1 |
| 1 |
| 1 |
d) 1152 - (374 + 1152) + (-65 + 374) = 1152 - 374 - 1152 + (-65) + 374 = (1152 - 1152) + (-65) + (374 - 374) = -65 | 1 |
e) 13 - 12 + 11 + 10 - 9 + 8 - 7 - 6 + 5 - 4 + 3 + 2 - 1 = = 13 - (12 - 11 - 10 + 9) + (8 - 7 - 6 + 5) - (4 - 3 - 2 + 1) = 13 | 1 |
Bài 2 : (4 điểm) Tìm x :
Câu | Đáp án | Điểm |
a. |
| 1 |
b. |
| 1 |
c. | 11 - (-53 + x) = 97
| 1 |
d. | -(x + 84) + 213 = -16
| 1 |
Bài 3 : (3 điểm)
Đáp án | Điểm |
Từ dữ liệu đề bài cho, ta có : + Vì ƯCLN(a, b) = 15, nên ắt tồn tại các số tự nhiên m và n khác 0, sao cho: a = 15m; b = 15n (1) và ƯCLN(m, n) = 1 (2) + Vì BCNN(a, b) = 300, nên theo trên, ta suy ra :
+ Vì a + 15 = b, nên theo trên, ta suy ra : Trong các trường hợp thoả mãn các điều kiện (2) và (3), thì chỉ có trường hợp : m = 4, n = 5 là thoả mãn điều kiện (4). Vậy với m = 4, n = 5, ta được các số phải tìm là : a = 15 . 4 = 60; b = 15 . 5 = 75 | 3 |
Bài 4 : (2 điểm)
Câu | Đáp án | Điểm |
a. | Chứng minh đẳng thức: - (-a + b + c) + (b + c - 1) = (b - c + 6) - (7 - a + b) + c. Biến đổi vế trái của đẳng thức, ta được : VT = -(-a + b + c) + (b + c - 1) = -(-a) - (b + c) + (b + c) + (-1) = a - 1 Biến đổi vế phải của đẳng thức, ta được : VP = (b - c + 6) - (7 - a + b) + c = b + (-c) + 6 - 7 + a - b + c = [b + (-b)] + [(-c) + c] + a + [6 + (-7)] = a - 1 So sánh, ta thấy : VT = VP = a - 1 Vậy đẳng thức đã được chứng minh. | 1 |
b. | Với a > b và S = -(-a - b - c) + (-c + b + a) - (a + b), ta có :
Tính * Xét với a và b cùng dấu, ta có các trường hợp sau xảy ra : + a và b cùng dương, hay a > b > 0, thì a + b > 0 : + a và b cùng âm, hay 0 > a > b, thì a + b < 0
* Xét với a và b khác dấu : Vì a > b, nên suy ra : a > 0 và b < 0 + + Vậy, với : + + | 1 |
Bài 5 : (6 điểm)
Câu | Đáp án | Điểm |
Hình vẽ |
|
|
a. | Hai tia AO, AB đối nhau, nên điểm A nằm giữa hai điểm O và B, suy ra :
| 2 |
b. | Ta có M và N thứ tự là trung điểm của OA, OB, nên :
Vì OA < OB, nên OM < ON. Hai điểm M và N thuộc tia OB, mà OM < ON, nên điểm M nằm giữa hai điểm O và N. | 2 |
c. | Vì điểm M nằm giữa hai điểm O và N, nên ta có :
suy ra : hay : Vì AB có độ dài không đổi, nên MN có độ dài không đổi, hay độ dài đoạn thẳng MN không phụ thuộc vào vị trí của điểm O (O thuộc tia đối của tia AB). | 2 |
ĐỀ THI SỐ 4
Câu 1 (6 điểm): Thực hiện các phép tính
a) ![]()
b) [528: (19,3 - 15,3)] + 42(128 + 75 - 32) – 7314
c) ![]()
Câu 2 (4 điểm): Cho A = 1 - 2 + 3 - 4 + 5 - 6+ ... + 19 - 20
a) A có chia hết cho 2, cho 3, cho 5 không?
b) Tìm tất cả các ước của A.
Câu 3 (4 điểm):
a) Chứng minh rằng: Hai số lẻ liên tiếp bao giờ cũng nguyên tố cùng nhau.
b) Tìm x biết: 1 + 5 + 9 + 13 + 16 +...+ x = 501501
Câu 4 (6 điểm): Cho tam giác ABC có BC = 5cm. Trên tia đối của tia CB lấy điểm M sao cho CM = 3cm.
a) Tính độ dài BM.
b) Cho biết ![]() = 800,
= 800, ![]() =600. Tính
=600. Tính ![]() .
.
c) Lấy K thuộc đoạn thẳng BM sao cho CK = 1cm. Tính độ dài BK.
ĐÁP ÁN
Câu 1 (6 điểm): Thực hiện các phép tính
a) (2 điểm):
= ![]()
b) (2 điểm):
= (528 : 4) + 42. 171 - 7314
= 132 + 7182 - 7314 = 0
c) (2 điểm):
= ![]()
= ![]()
Câu 2 (4 điểm):
a) (2 điểm):
A = (1-2) + (3-4) + (5-6) +...+ (19-20) (có 10 nhóm) (0,5đ)
= (-1) + (-1) + (-1) +...+ (-1) (có 10 số hạng) (0,5đ)
= 10. (-1) = -10 (0,5đ)
![]() Vậy A
Vậy A![]() 2, A
2, A ![]() 3, A
3, A ![]() 5. (0,5đ)
5. (0,5đ)
b) (2 điểm):
Các ước của A là: ![]() 1,
1, ![]() 2,
2, ![]() 5,
5, ![]() 10. (nêu được mỗi ước cho 0,25đ)
10. (nêu được mỗi ước cho 0,25đ)
Câu 3 (4 điểm):
a) (2 điểm):
Hai số lẻ liên tiếp có dạng 2n + 1 và 2n + 3 (n ![]() N). (0,5đ)
N). (0,5đ)
Gọi d là ước số chung của chúng. Ta có: 2n + 1![]() d và 3n + 3
d và 3n + 3 ![]() d (0,5đ)
d (0,5đ)
nên (2n + 3) - (2n + 1) ![]() d hay 2
d hay 2![]() d
d
nhưng d không thể bằng 2 vì d là ước chung của 2 số lẻ. (0,5đ)
Vậy d = 1 tức là hai số lẻ liên tiếp bao giờ cũng nguyên tố cùng nhau. (0,5đ)
b) (2 điểm)
Ta có: 5 = 2 + 3; 9 = 4 + 5; 13 = 6 + 7; 16 =7 + 8 ... (0,5đ)
Do vậy x = a + (a+1) (a ![]() N) (0,25đ)
N) (0,25đ)
Nên 1 + 5 + 9 + 13 + 16 +...+ x = 1+2+3+4+5+6+7+...+a+(a+1) = 501501 (0,25đ)
Hay (a+1)(a+1+1): 2 = 501501 (0,25đ)
(a+1)(a+2) = 1003002 = 1001 . 1002 (0,25đ)
Suy ra: a = 1000 (0,25đ)
Do đó: x = 1000 + (1000 + 1) = 2001. (0,25đ)
Câu 4 (6 điểm):
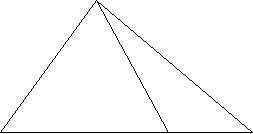
a) (2 điểm): Hai điểm M và B thuộc hai tia đối nhau
CM và CB nên điểm C nằm giữa hai điểm B và M (1đ)
Do đó: BM= BC + CM = 5 + 3 = 8 (cm) (1đ)
b) (2 điểm): Do C nằm giữa hai điểm B và M
![]() nên tia AC nằm giữa hai tia AB và AM (1đ)
nên tia AC nằm giữa hai tia AB và AM (1đ)
![]()
![]()
![]()
![]() Do đó
Do đó ![]() = 800 - 600 = 200 (1đ)
= 800 - 600 = 200 (1đ)
c) (2 điểm):
+ Nếu K thuộc tia CM thì C nằm giữa B và K (ứng với điểm K1 trong hình vẽ) (0,5đ)
Khi đó BK = BC + CK = 5 + 1 = 6 (cm) (0,5đ)
+ Nếu K thuộc tia CB thì K nằm giữa B và C (ứng với điểm K2 trong hình vẽ) (0,5đ)
Khi đó BK = BC - CK = 5 - 1 = 4 (cm) (0,5đ)
![]()
ĐỀ SỐ 6
Câu 1(3,0 điểm): Tính giá trị của các biểu thức sau:
a. ![]()
b. ![]()
Câu 2(4,0 điểm): Tìm các số nguyên x biết.
a. ![]()
b. ![]()
c. ![]()
Câu 3(5,0 điểm):
a, Một số tự nhiên chia cho 7 dư 5,chia cho 13 dư 4. Nếu đem số đó chia cho 91 thì dư bao nhiêu?
b, Học sinh khối 6 khi xếp hàng; nếu xếp hàng 10, hàng 12, hàng15 đều dư 3 học sinh. Nhưng khi xếp hàng 11 thì vùa đủ. Biết số học sinh khối 6 chưa đến 400 học sinh.Tính số học sinh khối 6?
Câu 4(6,0 điểm):
Cho góc bẹt xOy. Trên cùng một nửa mặt phẳng có bờ xy,vẽ các tia Oz và Ot sao cho ![]() .
.
a. Chứng tỏ tia Oz nằm giữa hai tia Ox và Ot ?
b. Chứng tỏ tia Ot là tia phân giác của góc yOz?
c.Vẽ tia phân giác On của góc xOz. Tính góc nOt?
Câu 5(2,0 điểm):
Cho n là số nguyên tố lớn hơn 3. Hỏi n2 + 2006 là số nguyên tố hay là hợp số.
---------Hết---------
ĐÁP ÁN
Câu
| Nội dung | Thang điểm |
Câu 1(4điểm) a (1,5) |
| 0.5 0.5
0.5
|
b (1,5) |
| 0.5
0.5
0,25
0.25 |
câu 2 (4điểm)
a (1,0) |
| 0.5
0.5 |
b (1,5) |
(không thỏa mãn) | 0.5
0.5
0.5 |
|
|
|
c (1,5) |
Vậy |
0.5
0.5 0.5 |
Câu3(4,0)
a (2,0) | Gọi số đó là a Vì a chia cho 7 dư 5, chia cho 13 dư 4
Vậy a chia cho 91 dư 82. | 0.25
1.0
1.0 0.25 |
b (2,0)
| Gọi số Hs khối 6 là a (3<a<400) Vì khi xếp hàng 10,hàng 12, hàng 15 đều dư 3
Vậy số HS khối 6 là 363 học sinh. | 0.25
0.5
0.5
0.75
0.5 |
Câu 4 (6,0)
Vẽ hình
|
n
xOy
|
0.5 |
a (1,5) | Vì góc xOy là góc bẹt nên suy ra trên cùng một nưả mặt phẳng có bờ xy có
Trên cùng một nửa mặt phẳng có bờ chứa tia Ox có:
|
0.75
0.75 |
b (2,0) | Trên cùng một nửa mặt phẳng có bờ xy ,ta có và
Trên cùng một nửa mặt phẳng có bờ chứa tia Oy có:
|
0.75
0.75
0.5
|
c (2,0) | Vì
Vì On là tia phân giác của góc xOz nên Ta lại có tia Ot là tia phân giác của góc yOz (theo b,)
|
0.5
0.5
0.5
0.5
|
C©u 5 (2,0) | n là số nguyên tố, n > 3 nên n không chia hết cho 3. Vậy n2 chia hết cho 3 dư 1 do đó n2 + 2006 = 3m + 1 + 2006 = 3m+2007 = 3( m+669) chia hết cho 3. Vậy n2 + 2006 là hợp số.
| 0.5 0.5
0.75
0.25
|