Đề kiểm tra 45 phút Toán 6 Chương 1 (Đề 1)
Bài 1. (3 điểm) Thực hiện phép tính :
a) 110700 : 15 . [ 356 – ( 2110 – 2000 )]
b) 62500 : { 502 : [ 112 – ( 52 – 23 . 5 )]}
c) 33 . 53 – 20 . { 300 – [ 540 – 23 ( 78 : 76 + 70 )]}
Bài 2. (2điểm) Tìm x ∈ N, biết :
a) 5x – 2x = 25 + 19
b) x200 = x
Bài 3. (2 điểm) Trong một phép chia có số bị chia là 410. Số dư là 19. Tìm số chia và thương.
Bài 4. (2 điểm) Một đoàn xe lửa dài 160 m chạy vào một đường hầm xuyên qua núi với vận tốc 40 km/h. Từ lúc toa đầu tiên bắt đầu chui và hầm đến lúc toa cuối cùng ra khỏi hầm mất 4 phút 30 giây. Hỏi đường hầm dài bao nhiêu km?
Bài 5. (1 điểm) Tổng của n số tự nhiên chẵn từ 2 đến 2n có thể là một số chính phương không ? Vì sao ? (Chú ý: Số chính phương là số bằng bình phương của một số tự nhiên)
Đáp án và Hướng dẫn giải
Bài 1.
a) 11070 : 15[ 356 – 110 ] = 11070 : 3690 = 3
b) 62500 : { 2500 : [ 112 – ( 52 – 8 . 5 )]}
= 62500 : { 2500 : [ 112 – ( 52 – 40 )]}
= 62500 : { 2500 : [ 112 – 12 ]}
= 62500 : { 2500 : 100 }
= 62500 : 25
= 2500
c) 33 . 53 – 20 . { 300 – [ 540 – 23 ( 78 : 76 + 70 )]}
= 33 . 53 – 20 . {300 – [ 540 – 23(72 + 1 )]
= 33 . 53 – 20 . [ 300 – (540 - 8 . 50)
= 27 . 125 – 20 . [300 – ( 540 - 400 )]
= 3375 – 20 . ( 300 – 140 )
= 3375 – 20 . 160
= 3375 – 3200
= 175
Bài 2.
a) 5x – 2x = 25 + 19
3x = 32 + 1
3x = 33
x = 11
b) x200 = x
x200 – x = 0
x ( x199 – 1) = 0
x = 0 hoặc x199 – 1 = 0
x = 0 hoặc x199 = 1
x = 0 hoặc x = 1
Bài 3.
Gọi a, b, q, r lần lượt là số bị chia, số chia, thương, số dư
Ta có: a = bq + r ( b ≠ 0 và 0 < r < b)
410 = bq + 19
bq = 410 – 19 = 391
Mà : 391 = 391 . 1 = 23 . 17
Vì b > r = 19 nên ta chọn b = 391 hoặc b = 23
- Số chia là 391 thì thương là 1
- Số chia là 23 thì thương là 17
Bài 4.
4 phút 30 giây = 270 giây
40 km/h = 40000 m/3600 giây
Trong 270 giây đoàn xe lửa chạy được : (40000 . 270) : 3600 = 3000 (m)
3000 m là chiều dài của đoàn tàu cộng với chiều dài của đường hầm.
Do vậy đường hầm dài: 3000 – 160 = 2840 (m)
Bài 5.
Ta có: 2 + 4 + 6 +… + ( 2n ) = ( 2n + 2 ) . n : 2 = n ( n+1 )
Mà n . n < n ( n+1 ) < ( n + 1 )( n + 1 ) ⇒ n2 < n ( n + 1 ) < ( n + 1 )2
n2 và (n + 1)2 là số chính phương liên tiếp nên n ( n + 1 ) không thể là số chính phương. Ta có điều cần chứng minh.
Đề kiểm tra 45 phút Toán 6 Chương 1 (Đề 2)
Bài 1. (3 điểm) Viết kết quả phép tính sau dưới dạng một lũy thừa :
a) 62010 : 610
b) (38 . 316 ) : (37 . 314 )
c) (226 : 210 ) : (218 : 216 )
d) 253 : 125
Bài 2. (2 điểm) Tích của hai số là 2610. Nếu thêm 5 đơn vị vào một thừa số thì tích mới sẽ là 2900. Tìm hai số đó.
Bài 3. (2điểm) Trong một phép chia số tự nhiên cho số tự nhiên, số bị chia là 236 và số dư là 15. Tìm số chia và thương.
Bài 4. (2 điểm )Tìm các thừa số và tích của các phép nhân sau :
![]()
Bài 5. (1 điểm) Tìm số tự nhiên nhỏ nhất, biết rằng khi chia số này cho 37 dư 1 và khi chia cho 39 dư 14.
Đáp án và Hướng dẫn giải
Bài 1.
a) 62010 : 610 = 62000
b) (38 . 316 ) : (37 . 314 ) = 324 : 321 = 33
c) (226 : 210 ) : (218 : 216 ) = 216 : 22 = 214
d) 253 : 125 = ( 25 . 25 . 25 ) : 53 = 56 : 53 = 53
Bài 2.
Tích mới hơn tích cũ là : 2900 – 2610 = 290
Tích mới hơn tích cũ 290 vì được thêm 5 lần thừa số kia
Thừa số kia là : 290 : 5 = 58
Thừa số này là : 2610 : 58 = 45
Bài 3.
Gọi a, b, q, r lần lượt là số bị chia, số chia, thương, số dư
Ta có: a = bq + r (b ≠ 0 và 0 < r < b)
236 = bq + 15
bq = 236 – 15 = 221
Mà : 221 = 221.1 = 13.17. Vì b > r = 15 nên ta chọn b = 221 hoặc b = 17
- Số chia là 221 thì thương là 1
- Số chia là 17 thì thương là 13
Bài 4.
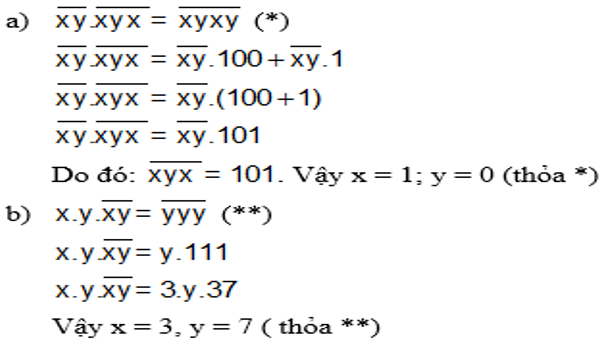
Bài 5.
Gọi số cần tìm là a. Gọi thương của phép chia số a lần lượt cho 37, 39 là h, k.
Ta có: a = 37h + 1 ; a = 39k + 14 và h ≠ k
37h + 1 = 39k + 14
37h – 37k = 2k + 13
37(h – k) = 2k + 13
Vì 2k + 13 là số tự nhiên lẻ nên 37 ( h – k ) là số tự nhiên lẻ
Do đó: h – k là số tự nhiên lẻ, suy ra h – k ≥ 1
a là số nhỏ nhất nên k nhỏ nhất, khi đó 2k nhỏ nhất
Do đó h – k nhỏ nhất nên h – k = 1
Ta có : 2k + 13 = 37 . 1 ⇒ 2k = 24 ⇒ k = 12. Khi đó: a = 39 . 12 + 14 = 482
Vậy a = 482
Đề kiểm tra 45 phút Toán 6 Chương 1 (Đề 3)
Bài 1. (2 điểm) Tìm ƯCLN của :
a) 30 , 45 , 135
b) 144 , 504 , 1080
Bài 2. (2 điểm) Tìm các số tự nhiên có ba chữ số, biết rằng khi chia số đó cho 8 thì dư 7, chia cho 31 thì dư 28
Bài 3. (2 điểm) Thay a, b bởi chữ số thích hợp để số ![]() chia hết cho cả 2, 5 và 9.
chia hết cho cả 2, 5 và 9.
Bài 4. (3 điểm)
a) Tìm hai số tự nhiên liên tiếp có tích bằng 650.
b) Tìm ba số tự nhiên liên tiếp có tích bằng 35904.
Bài 5. (1 điểm) Tìm số tự nhiên nhỏ nhất có bốn chữ số. Biết rằng khi chia số đó cho các số 70 ; 210 ; 350 có cùng số dư là 3.
Đáp án và Hướng dẫn giải
Bài 1.
a) 30 = 2 . 3 . 5
45 = 32 . 5
135 = 33 . 5
Vậy ƯCLN (30 ; 45 ; 135) = 3 . 5 = 15
b) 144 = 24 . 32
504 = 23 . 32 . 7
1080 = 23 . 33 . 5
Vậy ƯCLN (144 ; 504 ; 1080) = 23 . 32 = 72
Bài 2.
Gọi n là số cần tìm. Ta có: n + 1 ⋮ 8, do đó n + 65 ⋮ 8
Mặt khác: n + 3 ⋮ 31, do đó n + 65 ⋮ 31
Vậy n + 65 là bội chung của 8 và 31 và n + 65 < 1065
Các bội chung của 8 và 31 nhỏ hơn 1065 là : 248 ; 496 ; 744 ; 992.
Do đó n + 65 ∈ { 248 ; 496 ; 744 ; 992 }.
Vậy n ∈ { 183 ; 431; 679 ; 927 }
Bài 3.
a) 650 = 2 . 52 . 13 = 52 . ( 2 . 13 ) = 25 . 26
b) 35904 = 26 . 3 . 11 . 17 = 25 . ( 3 . 11 ) . ( 2 . 17 ) = 32 . 33 . 34
Bài 4.
Ta có: 273 chia cho a dư 3 nên 270 ⋮ a
2271 chia cho a dư 3 nên 2268 ⋮ a
1785 chia cho a dư 3 nên 1782 ⋮ a
Do đó a ∈ ƯC(270; 2268; 1782)
270 = 2 . 33 . 5
2268 = 22 . 34 .7
1782 = 2 . 34 . 11
ƯCLN ( 270 ; 2268 ; 1782 ) = 2 . 33 = 54
ƯC( 270 ; 2268 ; 1782 ) = Ư(54) = {1 ; 2 ; 3 ; 6 ; 9 ; 18 ; 27 ; 54}
Vì a có hai chữ số và nhỏ hơn 30 nên a ∈ {18; 27}
Vậy số cần tìm là 18 và 27.
Bài 5.
Gọi số cần tìm là a. Ta có : a – 3 chia hết cho 70 ; 210 ; 350
Do đó a – 3 ∈ BC(70; 210 ; 350) = {70 ; 140 ; ... ; 980 ; 1050 ;...}
Vì a là số nhỏ nhất có 4 chữ số nên : a – 3 = 1050 hay a = 1053.
Vậy số cần tìm là 1053.
Đề kiểm tra 45 phút Toán 6 Chương 1 (Đề 4)
Bài 1. (3 điểm) Các số tự nhiên nhỏ hơn 1000, có bao nhiêu số :
a) Chia hết cho 2
b) Chia hết cho 5
c) Chia hết cho 2 nhưng không chia hết cho 5.
Bài 2. (2 điểm) Tính số lượng các ước của các số sau. Sau đó hãy viết tập hợp các ước của số đó
a) 72
b) 120
Bài 3. (2 điểm) Học sinh khối 6 của một trường tập chung dưới sân trường để chào cờ. Nếu xếp theo hàng 20; 25; 30 thì đều dư 12 học sinh, nhưng nếu xếp hàng 26 thì vừa đủ. Tính số học sinh khối lớp 6 này,biết rằng số học sinh này ít hơn 700 học sinh
Bài 4. (1,5 điểm) Tìm số tự nhiên x lớn nhất, biết rằng 428 và 708 chia cho x được số dư là 8.
Bài 5. (1,5 điểm) Tìm số tự nhiên nhỏ nhất chia cho 3, cho 4, cho 5 thì có số dư lần lượt là 1, 3, 1.
Đáp án và Hướng dẫn giải
Bài 1.
a) Tập hợp các số chia hết cho 2 nhỏ hơn 1000 là { 0 ; 2 ; 4 ; ... ; 996 ; 998 }
Số các phần tử thuộc tập hợp trên là: ( 998 – 0 ) : 2 + 1 = 500 (phần tử)
b) Tập hợp các số chia hết cho 5 nhỏ hơn 1000 là { 0 ; 5 ; 10 ;... ; 990 ; 995 }
Số các phần tử thuộc tập hợp trên là: ( 995 – 0 ) : 5 + 1 = 200 (phần tử)
c) Trong một chục có 4 số chia hết cho 2 nhưng không chia hết cho 5.
Từ 0 đến 999 có 100 chục nên ta có: 4 . 100 = 400 (số)
Số 1000 không phải đếm.
Vậy cả 400 số chia hết cho 2 nhưng không chia hết cho 5.
Bài 2.
a) 72 = 23 . 32 có (3 + 1) . (2 + 1) = 12 (ước)
Ư(72) = {1; 2; 3; 4; 6; 8; 9; 12; 18; 24; 36; 72}
b) 120 = 23 . 3 . 5 có ( 3 + 1 ) . ( 1 + 1 ) . ( 1 + 1 ) = 16 (ước)
Ư(120) = {1; 2; 3; 4; 5; 6; 8; 10; 12; 15; 20; 24; 30; 40; 60; 120}
Bài 3.
Số học sinh khối 6 của trường là bội chung của 20; 25; 30.
20 = 22 . 5 ;
30 = 2 . 3 . 5 ;
25 = 52
BCNN( 20 ; 25 ; 30 ) = 22 . 3 . 52 = 300
BC ( 20; 25; 30 ) = B ( 300 ) = { 0; 300; 600; 900; 1200;… }
Số học sinh khối 6 của trường có thể là 12; 312; 612; 912; 1212…
Vì số học sinh đó là số chia hết cho 26 và chưa đến 700 nên số học sinh đó là 312 học sinh.
Bài 4.
Theo đề bài, ta có:
428 – 8 = 420 chia hết cho x
708 – 8 = 700 chia hết cho x (x ∈ N, x > 8) và x lớn nhất
Do đó x là ước chung lớn nhất của 420, 700
420 = 22 . 3 . 5 . 7 ;
700 = 22 . 52 . 7
ƯCLN ( 420 ; 700 ) = 22 . 5 . 7 = 140
Vậy x = 140.
Bài 5.
Gọi n là số cần tìm.
Ta có: n – 1 là bội của 3, n – 3 là bội của 4, n – 1 là bội của 5
Suy ra: 2( n – 1) ⋮ 3 ;
2(n – 3) ⋮ 4 ;
2(n – 1) ⋮ 5
Do đó: 2n chia cho 3, 4, 5 đều dư 2. Nên 2n – 2 là BCNN của 3, 4, 5
2n – 2 = 60 ⇒ n = 31.