Giải SBT Toán 7 Bài 5: Lũy thừa của một số hữu tỉ
Bài 39 trang 14 sách bài tập Toán 7 Tập 1: Tính:
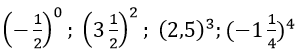
Lời giải:
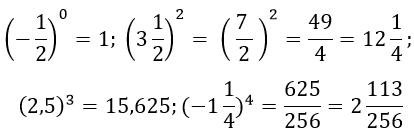
Bài 40 trang 15 sách bài tập Toán 7 Tập 1: Viết các số sau dưới dạng luỹ thừa với số mũ khác 1
125; -125; 27; -27
Lời giải:
125 = 53; -125=(-5)3;27=33; -27= (-3)3
Bài 41 trang 15 sách bài tập Toán 7 Tập 1: Tìm số 25 dưới dạng luỹ thừa. Tìm tất cả các cách viết
Lời giải:
25 = 251 = 52=(-5)2
Bài 42 trang 15 sách bài tập Toán 7 Tập 1: Tìm x ∈ Q, biết rằng:
a. (x - (1/2))2 = 0
b. (x - 2)2 = 1
c. (2x - 1)3 = -8
d. (x + (1/2))2 = 1/16
Lời giải:
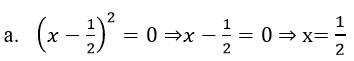
b. (x-2)2 = 1 => x- 2 = 1 => x = 3
c. (2x-1)3 = -8 => (2x-3)3 = (-2)3 => 2x – 1 = -2 => x= -1/2
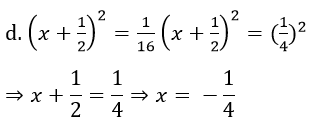
Bài 43 trang 15 sách bài tập Toán 7 Tập 1: So sánh: 2225 và 3150
Lời giải:
2225 = 23.75 = (23)75 = 875
3150 = 32.75 = (32)75=975
8 < 9 => 875 < 975
Vậy : 2225 < 3150
Bài 44 trang 15 sách bài tập Toán 7 Tập 1: Tính
a. 253 : 52
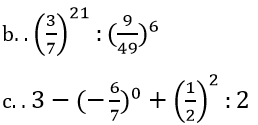
Lời giải:
a. 253 : 52 = 253 : 25= 252 = 625
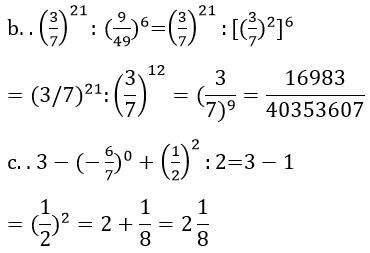
Bài 45 trang 15 sách bài tập Toán 7 Tập 1: Viết các biểu thức sau dưới dạng an (a ∈ Q, n ∈ N )
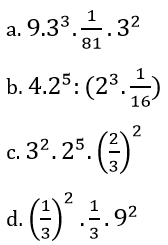
Lời giải:
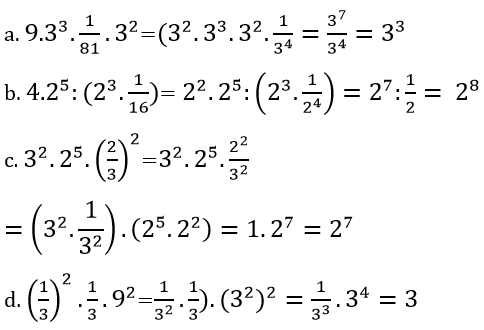
Bài 46 trang 15 sách bài tập Toán 7 Tập 1: Tìm tất cả các số tự nhiên n sao cho:
a) 2.16 ≥ 2n > 4
b) 9.27 ≤ 3n ≤ 243
Lời giải:
a) 2.16 ≥ 2n > 4 => 2. 24 ≥ 2n > 22
=>2 < n ≤ 5 => n ∈ {3; 4; 5}
b) 9.27 ≤ 3n ≤ 243 => 32.33 ≤ 3n ≤ 35
=> 35 ≤ 3n ≤ 35 => n = 5
Bài 47 trang 16 sách bài tập Toán 7 Tập 1: chứng minh rằng: 87 - 218 chia hết cho 14
Lời giải:
Ta có: 87 - 217 = (23)7 - 218 = 217.( 24 -2)= 217.(16 - 2)
= 24.14 ⋮ 14
Bài 48 trang 16 sách bài tập Toán 7 Tập 1: So sánh: 291 và 535
Lời giải:
Ta có: 291 > 290= (25)18 = 3218 (1)
3218 > 2518 (2)
2518 = (52)18= 536 > 535 (3)
Từ (1), (2) và (3) suy ra: 291 > 535
Bài 49 trang 16 sách bài tập Toán 7 Tập 1: Hãy chọn câu trả lời đúng trong các câu sau A, B, C, D, E:
a. 36.32
A. 34 B. 38 C. 312 D. 98 E. 912
b. 24.22.23=
A. 29 B. 49 C. 89 D. 224 E. 824
c. an.a2
A. an-2 B. (2a)n+2 C. (a.a)2n
D. an+2 E. a2n
d. 36 : 32
A. 38 B. 14
C. 3-4 D. 312 E. 34
Lời giải:
a) 36.32 = 38
Vậy chọn đáp án B
b) 24.22.23=29
Vậy có đáp án A
c) an.a2=an+2
Vậy chọn đáp án D
d) 36: 32=34
Vậy chọn đap án E
Bài 5.1 trang 16 sách bài tập Toán 7 Tập 1: Tổng 55 + 55 + 55 + 55 + 55 bằng:
(A) 255 ; (B) 525 ;
(C) 56 ; (D) 2525.
Hãy chọn đáp án đúng.
Lời giải:
Chọn (C) 56.
Bài 5.2 trang 16 sách bài tập Toán 7 Tập 1: Số x14 là kết quả của phép toán:
(A) x14: x ; (B) x7. x2 ;
(C) x8. x6 ; (D) x14 . x.
Hãy chọn đáp án đúng.
Lời giải:
Chọn (C)x8. x6.
Bài 5.3 trang 16 sách bài tập Toán 7 Tập 1: Tìm x, biết:
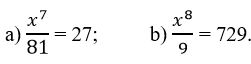
Lời giải:
a) x7/81 = 27 ⇒ x7 = 81.27 = 34. 33 = 37 ⇒ x = 3.
b) x8/9 = 729 ⇒ x8 = 9.729 = (±3)2. (±3)6 = (±3)8
⇒ x = ±3
Bài 5.4 trang 16 sách bài tập Toán 7 Tập 1: Tìm số nguyên n lớn nhất sao cho n150 < 5225.
Lời giải:
n150 = (n2)75 ; 5225 = (53)75 = 12575
n150 < 5225 hay (n2)75 < 12575. Suy ra n2 < 125.
Số nguyên lớn nhất thoả mãn điều kiện trên là n = 11.
Bài 5.5 trang 16 sách bài tập Toán 7 Tập 1: Tính: M = 22010 - (22009 + 22008 + ... + 21 + 20)
Lời giải:
Đặt A = 22009 + 22008 + ... + 21 + 20
Ta có 2A = 22010 + 22009 + ... + 22 + 21.
Suy ra 2A - A = 22010 - 20 = 22010 - 1.
Do đó M = 22010 - A = 22010 - (22010 - 1) = 1.
Bài 6 trang 17 sách bài tập Toán 7 Tập 1: So sánh 34000 và 92000 bằng hai cách.
Lời giải:
Cách 1: 92000 = (32)2000 = 34000
Cách 2: 34000 = (34)1000 = 811000. (1)
92000 = (92)1000 = 811000. (2)
Từ (1) và (2) suy ra 34000 = 92000 .
Bài 5.7 trang 17 sách bài tập Toán 7 Tập 1: So sánh 2332 và 3223.
Lời giải:
Ta có 3223 > 3222 = (33)111 = 9111. (1)
2332 < 2333 = (23)111 = 8111. (2)
Từ (1) và (2) suy ra: 2332 < 8111 < 9111 < 3223.
Vậy 2332 < 3223