Giải SBT Toán 7 Ôn tập chương 1 phần Đại số

Bài 130 trang 32 sách bài tập Toán 7 Tập 1: Tìm x biết

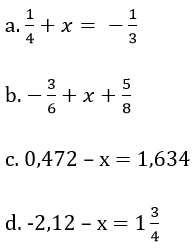
Lời giải:

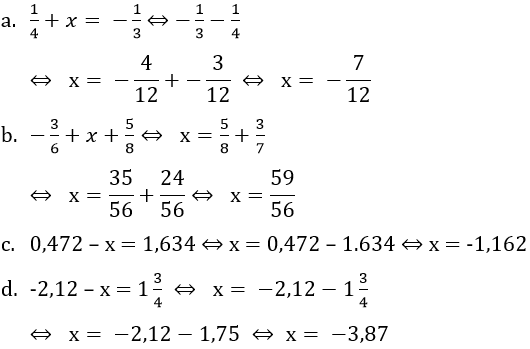
Bài 131 trang 33 sách bài tập Toán 7 Tập 1: Tìm số nghịch đảo của a biết:

a. a = 0,25;

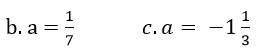
d. a = 0;

Lời giải:

a. Số nghịch đảo của a là 4;

b. Số nghịch đảo của a là 7;

c. Số nghịch đảo của a là -3/4;

d. a= 0 không có số nghịch đảo;

Bài 132 trang 33 sách bài tập Toán 7 Tập 1: Chứng minh rằng số nghịch đảo của một số hữu tỉ âm cũng là một số âm.

Lời giải:

Gọi số hữu tỉ âm là x, ta có x ≠ 0. Số nghịch đảo của x là 1/x

Vì ax.(1/x) = 1 > 0 nên x và (1/x) cùng dấu,mà x < 0 nên (1/x) < 0

Bài 133 trang 33 sách bài tập Toán 7 Tập 1: Tìm x trong các tỉ lệ thức sau:

a. x : (-2,14) = (-3,12) : 12

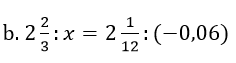
Lời giải:

a) x : (-2,14) = (-3,12) : 12

⇔ a.1,2 = ( -2,14).(-3,12) ⇔ x = 5,564

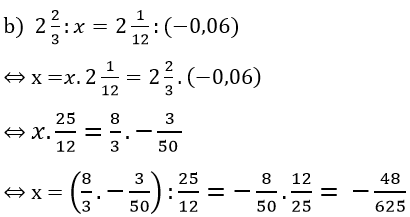
Bài 134 trang 33 sách bài tập Toán 7 Tập 1: Từ tỉ lệ thức

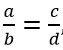
Hãy suy ra các tỉ lệ thức sau:

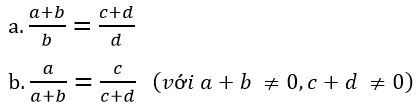
Lời giải:

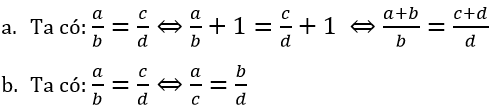
Theo tính chất dãy tỉ số bằng nhau ta có:

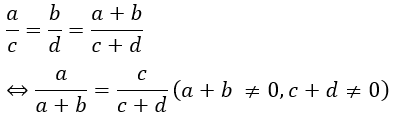
Bài 135 trang 33 sách bài tập Toán 7 Tập 1: Một mảnh đất hình chữ nhật có chu vi bằng 70m và tỉ số giữa hai cạnh của nó bằng 3/4. Tính diện tích miếng đất này

Lời giải:

Gọi chiều dài miếng đất là a, chiều rộng là b, ta có:

a + b = 70 : 2 = 35 và

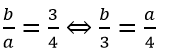
Theo tính chất dãy tỉ số bằng nhau ta có:

Chiều dài miếng đất là 20m và chiều rộng là 15m

Diện tích miếng đất là 300m²

Bài 136 trang 33 sách bài tập Toán 7 Tập 1: Hãy cho một ví dụ minh hoạ để bác bỏ mệnh đề sau: “Tổng của hai số vô tỉ là một số vô tỉ”

Lời giải:

√5+(-√5) = 0 ∈ Q

Bài 137 trang 33 sách bài tập Toán 7 Tập 1: a. Các đẳng thức sau có đúng không?

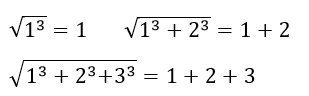
b, Hãy cho và kiểm tra hai đẳng thức như trên

Lời giải:

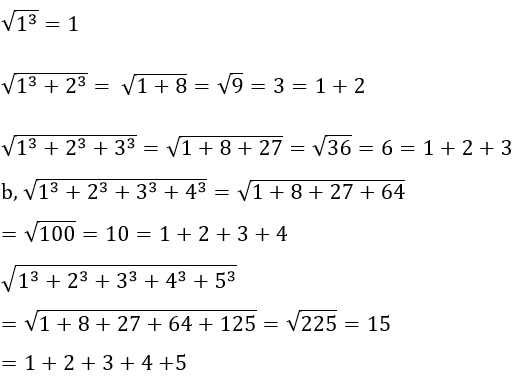
Bài 138 trang 33 sách bài tập Toán 7 Tập 1:

Lời giải:

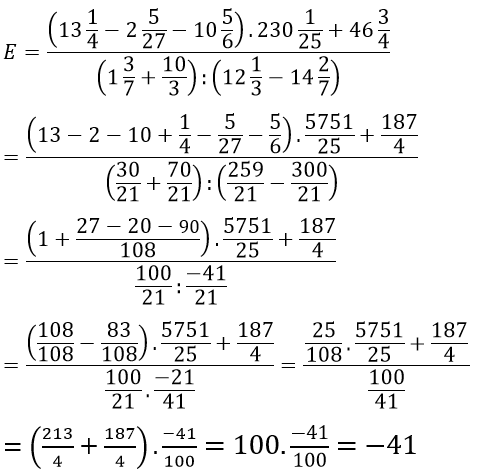
Bài 139 trang 34 sách bài tập Toán 7 Tập 1:

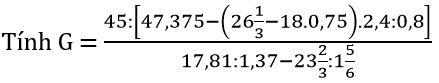
Lời giải:

Bài 140 trang 34 sách bài tập Toán 7 Tập 1: Cho x, y ∈ Q. Chứng tỏ rằng

a) |x + y| ≤ |x| + |y|.

b) |x - y| ≥ |x| - |y|.

Lời giải:

a) Với mọi x, y ∈ Q ta luôn có x ≤ |x| và -x ≤ |x|;

y ≤ |y| và -y ≤ |y| ⇒ x + y ≤ |x| + |y| và -x – y ≤ |x| + |y|

hay x + y ≥ -(|x| + |y|).

Do đó –(|x| + |y|) ≤ x + y ≤ |x| + |y|.

Vậy |x + y| ≤ |x| + |y|.

(Dấu “=” xảy ra khi xy ≥ 0.

b) Theo câu a ta có: |x - y| + |y| ≥ |x – y + y| = |x| ⇒ |x - y| ≥ |x| - |y|.

Bài 141 trang 34 sách bài tập Toán 7 Tập 1: Tìm giá trị nhỏ nhất của biểu thức:

A = |x – 2001| + |x -1|

Lời giải:

Vì |1 - x| = |x - 1| nên A = |x - 2001| + |x - 1|

= |x - 2001| + |1 - x| ≥| x – 2001 + 1 - x| =2000

Vậy giá trị nhỏ nhất của biểu thức A = 2000 khi x – 2001 và 1 – x cùng dấu

Vậy 1 ≤ x ≤ 2001

Bài I.1 trang 34 sách bài tập Toán 7 Tập 1: Tích 2⁵.9⁵.2⁸.9⁸ bằng:

(A) 11¹³ ;     (B) 11⁴⁰ ;

(C) 324²⁶ ;     (D) 18¹³.

Hãy chọn đáp án đúng.

Lời giải:

Chọn (D) 18¹³

Bài I.2 trang 34 sách bài tập Toán 7 Tập 1: Thương 12³⁰/36¹⁵ bằng:

(A) 4¹⁵ ;    (B) (1/3)¹⁵;

(C) (1/3)²;     (D) 1.

Hãy chọn đáp án đúng.

Lời giải:

Chọn (A) 4¹⁵.

Bài I.3 trang 34 sách bài tập Toán 7 Tập 1:

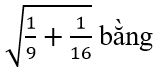
Hãy chọn đáp án đúng.

Lời giải:

Chọn (C) 5/12.

Bài I.4 trang 34 sách bài tập Toán 7 Tập 1: Cho a + b + c = a² + b² + c² = 1 và x : y : z = a : b : c.

²²²²

Lời giải:

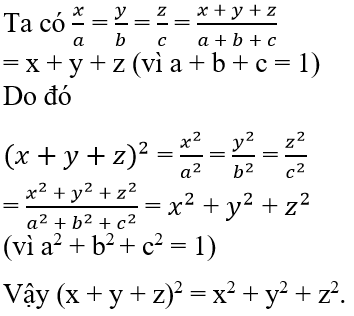
Bài I.5 trang 34 sách bài tập Toán 7 Tập 1: Tìm x, y biết

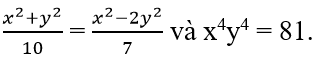
Lời giải:

Đặt x² = a (a ≥ 0), y² = b (b ≥ 0)

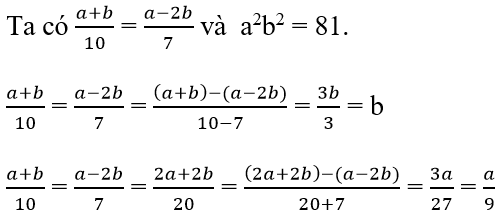
Từ (1) và (2) suy ra a/9 = b ⇒ a = 9b

Do a²b² = 81 nên (9b²).b² = 81 ⇒ 81b⁴ = 81 ⇒ b⁴ = 1 ⇒ b = 1 (vì b ≥ 0)

Suy ra a = 9 . 1 = 9

Ta có x² = 9 và y² = 1. Suy ra x = ±3, y = ±1.

Bài I.6 trang 35 sách bài tập Toán 7 Tập 1: Với giá trị nào của x thì A = |x − 3| + |x − 5| + |x − 7| đạt giá trị nhỏ nhất?

Lời giải:

Ta biết rằng |A| ≥ A (Dấu ''='' xảy ra khi và chỉ khi A ≥ 0)

|A| = |-A| và |A| ≥ 0 (Dấu ''='' xảy ra khi và chỉ khi A = 0)

Ta có A = |x − 3| + |x − 5| + |x − 7| ≥ x – 3 + 0 + 7 – x = 4

Dấu ''='' xảy ra khi và chỉ khi

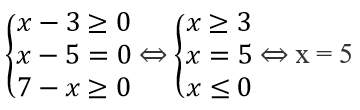
Vậy với x = 5 thì A đạt giá trị nhỏ nhất là 4.

Bài I.7 trang 35 sách bài tập Toán 7 Tập 1: Với giá trị nào của x thì B = |x − 1| + |x − 2| + |x − 3| + |x − 5| đạt giá trị nhỏ nhất?

Lời giải:

B = |x − 1| + |x − 2| + |3 − x| + |5 − x|

⇒ B ≥ x – 1 + x – 2 + 3 – x + 5 – x

Dấu ''='' xảy ra khi và chỉ khi

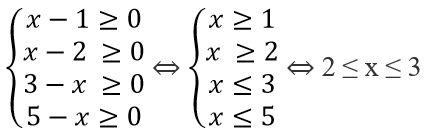
Vậy với 2 ≤ x ≤ 3 thì B đạt giá trị nhỏ nhất là 5.