Giải SBT Toán 7 Bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (g.c.g)

Bài 49 trang 144 sách bài tập Toán 7 Tập 1: Vẽ tam giác ABC biết ∠B =90^o,∠C =60^o, BC = 2cm. Sau đó đo AC để kiểm tra rằng AC = 4cm.

Lời giải:

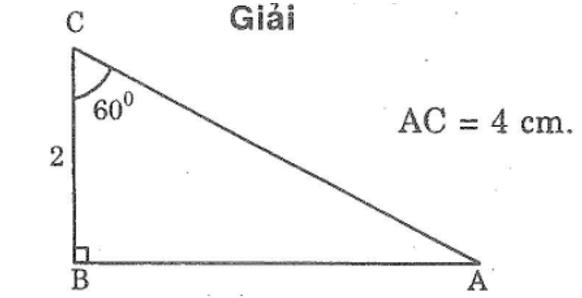
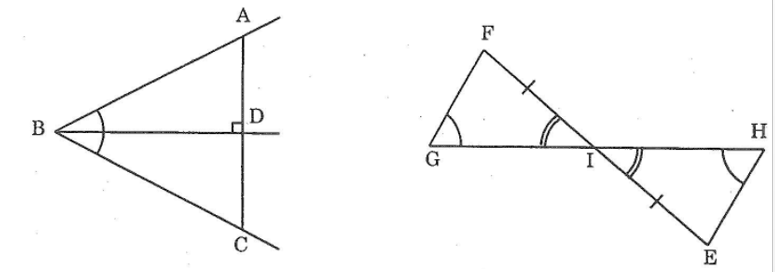
Bài 50 trang 144 sách bài tập Toán 7 Tập 1: Tìm các tam giác bằng nhau ở hình dưới (không xet tam giác mà các cạnh chưa được kẻ)

Lời giải:

Ta có: ΔABD= ΔCBD (g.c.g)

ΔGIF= ΔHIE (g.c.g)

Bài 51 trang 144 sách bài tập Toán 7 Tập 1: Cho tam giác ADE có ∠AD=∠AE . Tia phân giác của góc D cắt AE ở điểm M. tia phân giác của góc E cắt AD ở điểm N. So sánh các độ dịa DN và EM

Lời giải:

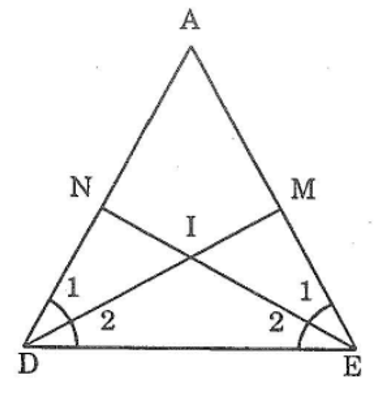
Tam giác ADE có: ∠D =∠E (gt)

∠(D₁ ) =∠(D₂ ) = (1/2)∠D (vì DM là tai phân giác)

∠(E₁ ) = ∠(E₂ ) = (1/2)∠E (vì EN là tia phân giác)

Suy ra: ∠(D₁ ) =∠(D₂ ) =∠(E₁ ) =∠(E₂ )

xét ΔDNE và ΔEMD, ta có:

∠(NDE) =∠(MED) (gt)

DE cạnh chung

∠(D₂ ) =∠(E₂ ) (chứng minh trên)

Suy ra: ΔDNE= ΔEMD (g.c.g)

Vậy DE = EM (hai góc tương ứng)

Bài 52 trang 144 sách bài tập Toán 7 Tập 1: Cho hình bên, trong dod AB // HK, AH // BK.Chứng minh rằng AB = HK; AH = BK

Lời giải:

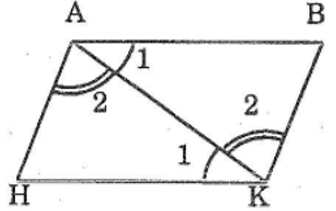
Nối AK, ta có:

AB // HK (gt)

⇒ ∠(A₁ ) =∠(K₁ ) (hai góc so le trong)

AH // BK (gt)

⇒ ∠ (A₂ ) =-∠(K₂ ) (hai góc so le trong)

Xét ΔABK và ΔKHA, ta có:

∠(A₁ ) =∠(K₁ )

AK canh chung

∠(A₂ ) =∠(K₂ )

Suy ra: ΔABK =ΔKHA (g.c.g)

Vậy: AB = KH; BK = AH ( 2 cạnh tương ứng)

Bài 53 trang 144 sách bài tập Toán 7 Tập 1: Cho tam giác ABC. Các tua phân giác của các góc B và C cắt nhau ở O. Kẻ OD⊥AC, kẻ OE⊥AB. Chứng minh rằng OD = OE

Lời giải:

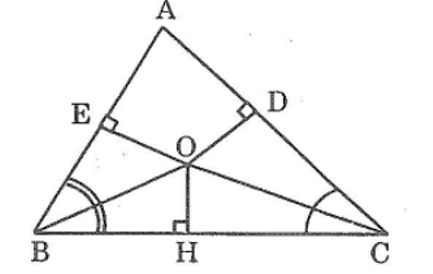
Kẻ OH⊥BC

Xét hai tam giác vuông OEB và OHB, ta có:

∠(OEB) =∠OHB=90^o

Cạnh huyền OB chung

∠(EBO) =∠(HBO)

Suy ra Δ OEB = Δ OHB (cạnh huyền góc nhọn)

⇒OE = OH (hai cạnh tương ứng)

Xét hai tam giác vuông OHC và ODC, ta có:

∠(OHC) =∠ODC=90^o

Cạnh huyền OB chung

∠(HCO) =∠(DCO)

Suy ra Δ OHC = Δ ODC (cạnh huyền góc nhọn)

⇒OD = OH (hai cạnh tương ứng)

Từ (1) và (2) suy ra: OE = OD

Bài 54 trang 144 sách bài tập Toán 7 Tập 1: Cho tam giác ABC có AB = AC. Lấy điểm D trân cạnh AB, điểm E trên cạnh AC sao cho AD = AE

a, Chứng minh rằng BE = CD

b, Gọi O là giao điểm của BE và CD

Chứng minh rằng ΔBOD=COE

Lời giải:

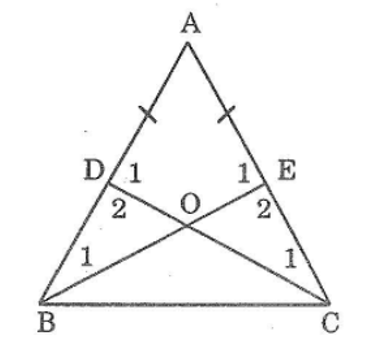
a. Xét ΔBEA và CDA, ta có:

BA = CA (gt)

∠A chung

AE=AD

Suy ra: ΔBEA= CDA (c.g.c)

Vậy: BE = CD (hai cạnh tương ứng)

b. ΔBEA= ΔCDA (chứng minh trên)

⇒∠(B₁ ) =∠(C₁ ) ;∠(E₁ ) =∠(D₁ ) (hai góc tương ứng)

∠(E₁ ) +∠(E₂ ) =180^o (hai góc kề bù)

∠(D₁ ) +∠(D₂ ) =180^o (hai góc kề bù)

Suy ra: ∠(E₂ ) =∠(D₂ )

AB = AC (gt)

⇒AE + EC = AD = BD MÀ AE = AD (GT)⇒EC = BD

Xét ΔODB và ΔOCE, ta có:

∠(E₂ ) =∠(D₂ ) (chứng minh trên)

DB=EC (chứng minh trên)

∠(B₁ ) =∠(C₁ )

Suy ra: ΔODB= ΔOCE

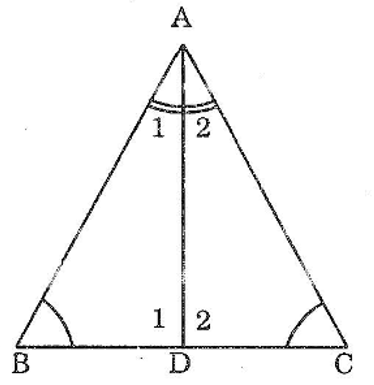
Bài 55 trang 145 sách bài tập Toán 7 Tập 1: Cho tam giác ABC có ∠B =∠C Tia phân giác của góc A cắt BC tại D

chứng minh rằng: BD = DC; AB = AC

Lời giải:

Trong ΔADB, ta có:

∠B +∠(A₁ ) +∠(D₁) =180^o (tổng 3 góc trong tam giác)

Suy ra: ∠(D₁ ) =180^o-(∠C +(A₁)) (1)

Trong ΔADC, ta có:

∠C +∠(A₂) +∠(D₂) =180^o (tổng 3 góc trong tam giác)

Suy ra: ∠(D₂) =180^o-(∠C +∠(A₂) ) (2)

∠B =∠C (gt)

∠(A₁ ) =∠(A₂) (gt)

Từ (1) và (2) và gt suy ra: ∠(D₁) =∠(D₂)

Xét ΔABD và ΔADC, ta có:

∠(A₁ ) =∠(A₂)(gt)

AD cạnh chung

∠(D₁ ) =∠(D₂)

Vậy: ΔABD= ΔADC (g.c.g)

Vậy: AB = AC (hai cạnh tương ứng)

DB = DC (hai cạnh tương ứng)

Bài 56 trang 145 sách bài tập Toán 7 Tập 1: Cho hình dưới, chứng minh rằng O là trung điểm của mỗi đoạn thẳng AD, BC

Lời giải:

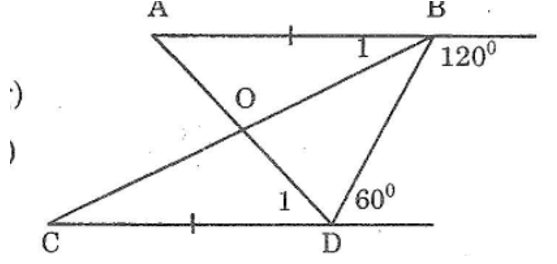
Hai đường thẳng AB và CD tạo với BD có hai góc trong cùng phía bù nhau: 120^o+60^o=180^o

Suy ra: AB // CD

Ta có: ∠A =∠(D₁) (hai góc so le trong)

∠C =∠(B₁) (hai góc so le trong)

AB = CD (gt)

Suy ra: Δ AOB= Δ DOC (g.c.g)

Suy ra: OA = OD; OB = OC (hai cạnh tương ứng)

Vậy O là trung điểm của mỗi đoạn thẳng AD và BC

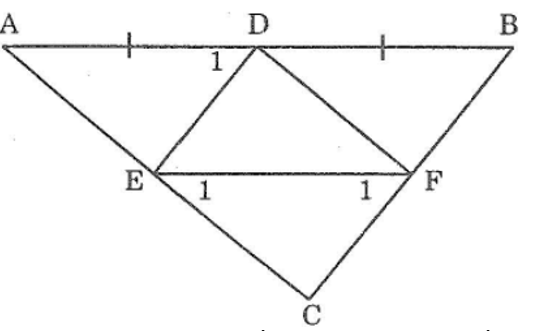
Bài 57 trang 145 sách bài tập Toán 7 Tập 1: Cho hình dưới trong đó DE // AB, DF // AC, EF // BC. Tính chu vi tam giác DFE

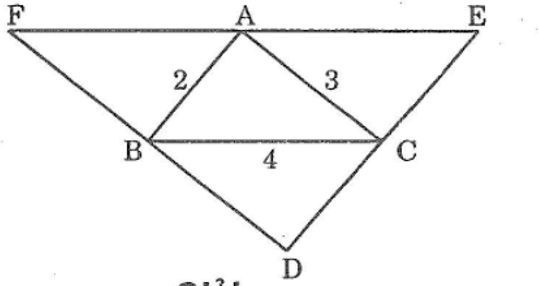
Lời giải:

Xét ΔABC và ΔABF, ta có:

∠(ABC) =∠(BAF) (so le trong)

AB cạnh chung

∠(BAC) =∠(ABF) (so le trong)

Suy ra: ΔABC= ΔABF(g.c.g)

Suy ra: AF = BC = 4 (hai cạnh tương ứng)

BF = AC = 3(hai cạnh tương ứng)

Xét ΔABC và ΔACE, ta có:

∠(ACB) =∠(CAE) (so le trong)

AC cạnh chung

∠(BAC) =∠(ECA) (so le trong)

Suy ra: ΔABC= ΔCEA(g.c.g)

Suy ra: AE = BC = 4(hai cạnh tương ứng)

CE = AB (hai cạnh tương ứng)

Xét ΔABC và ΔDCB, ta có:

∠(ACB) =∠(DBC) (so le trong)

BC cạnh chung

∠(ABC) =∠(DCB) (so le trong)

Suy ra: ΔABC= ΔDCB(g.c.g)

Suy ra: DC = AB = 2(hai cạnh tương ứng)

DB = AC (hai cạnh tương ứng)

Ta có: EF =AE=AF =4 + 4=8

DF = DB + BF = 3+ 3 =6

DE = DC + CE = 2 + 2 = 4

Vậy chu vi ΔDEF là:

DE + DF + EF = 4+ 6 + 8 =18 (đơn vị độ dài)

Bài 58 trang 145 sách bài tập Toán 7 Tập 1: Cho đoạn thẳng AB. Qua A vẽ đường thẳng m vuông góc với AB. Qua B vẽ đường thẳng n vuông góc với AB. Qua trung điểm O của AB vẽ một đường thẳng cắt m ở C và cắt n ở D. so sánh các độ dài OC và OD.

Lời giải:

Xét ΔAOC và ΔBOD ta có:

∠(CAO) =∠(DBO) =90^o

OA = OB

∠(AOC) =∠(BOD)

Suy ra: ΔAOC= ΔBOD(g.c.g)

Vậy: OC = OD

Bài 59 trang 145 sách bài tập Toán 7 Tập 1: Cho tam giác ABC có AB = 2,5cm, AC = 3 cm; BC = 3,5 cm. Qua A vẽ đươnhg thẳng song song với BC, qua C vẽ đường thẳng song song với AB, chúng cắt nhau tại D. tính chu vi tam giác ACD.

Lời giải:

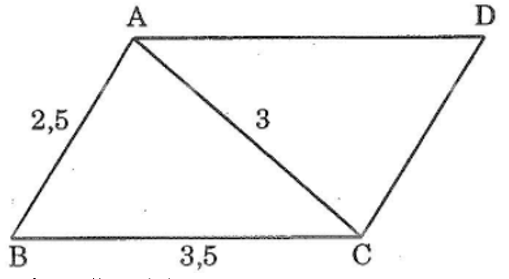
Ta có: AB // CD (gt)

Suy ra ∠(ACD) =∠(CAB) ̂(hai góc so le trong)

BC // AD (gt)

Suy ra: ∠(CAD) =∠(ACB) (hai góc so le trong)

Xét ΔABC và ΔCDA, ta có:

∠(CAD) =∠(ACB) (chứng minh trên)

AC cạnh chung

∠(ACD) =∠(CAB) (chứng minh trên)

Suy ra: ΔABC= ΔCDA (g.c.g)

Suy ra: CD = AB = 2,5cm và AD = BC = 3,5 cm

Chu vi ΔACD là : AC + AD + CD = 3 + 3,5 + 2,5 = 9 cm

Bài 60 trang 145 sách bài tập Toán 7 Tập 1: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC ở D. kẻ DE vuông góc vớ BC. Chứng minh rằng AB = BE

Lời giải:

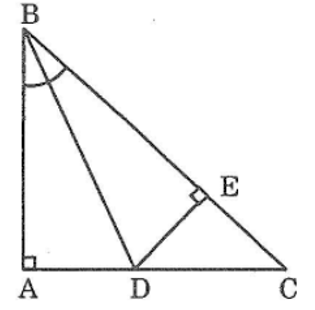
Xét hai tam giác vuông ABD và EBD, ta có:

∠(BAD) =∠(BED) =90^o

Cạnh huyền BD

∠(ABD) =∠(EBD) (gt)

Suy ra: Δ ABD= Δ EBD(cạnh huyền, góc nhọn)

Vậy BA = BE ( hai cạnh tương ứng)

Bài 61 trang 145 sách bài tập Toán 7 Tập 1: Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy (B, C nằm cùng phía đối với xy). Kẻ BD và CE vuông góc với xy. Chứng minh rằng:

a, ΔBAD= ΔACE

b, DE=BD+CE

Lời giải:

a, Ta có: ∠(BAD) +∠(BAC) +∠(CAE) =180^o(kề bù)

Mà ∠(BAC) =90^o (gt) ⇒∠(BAD) +∠(CAE) =90^o (1)

Trong ΔAEC, ta có: ∠(ACE) =90^o ⇒∠(CAE) +∠(ACE) =90^o (2)

Từ (1) và (2) suy ra: ∠(BAD) =∠(ACE)

Xét hai tam giác vuông AEC và BDA, ta có:

∠(AEC) +∠(DBA) =90^o

AC = AB (gt)

∠(ACE) +∠(BAD) (chứng minh trên)

Suy ra: ΔAEC= ΔBDA(cạnh huyền. Góc nhọn)

b, Ta có: ΔAEC= ΔBDA

⇒AE = BD và EC = DA

Mà DE = DA + AE

Vậy: DE = CE + BD

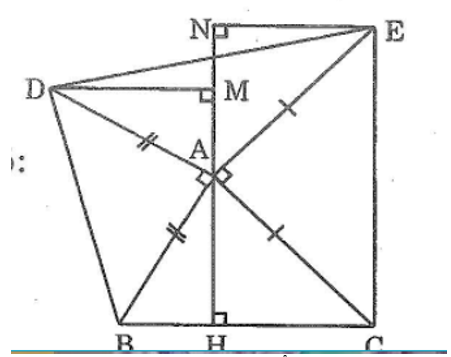
Bài 62 trang 145 sách bài tập Toán 7 Tập 1: Cho tam giác ABC. Vẽ ở phía ngoài tam giác ABC các tam giác vuông tại A và ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuoong góc với AH.

Chứng minh rằng:

a. DM = AH

b. MN đi qua trung điểm của DE

Lời giải:

a, Ta có: ∠(BAH) +∠(BAD) +∠(DAM) =180^o(kề bù)

Mà ∠(BAD) =90^o⇒∠(BAH) +∠(DAM) =90^o(1)

Trong tam giác vuông AMD, ta có:

∠(AMD) =90^o⇒∠(DAM) +∠(ADM) =90^o(2)

Từ (1) và (2) suy ra: ∠(BAH) =∠(ADM)

Xét hai tam giác vuông AMD và BHA, ta có:

∠(BAH) =∠(ADM)

AB = AD (gt)

Suy ra: ΔAMD= ΔBHA(cạnh huyền, góc nhọn)

Vậy: AH = DM (hai cạnh tương ứng) (3)

b, Ta có: ∠(HAC) +∠(CAE) +∠(EAN) =180^o(kề bù)

Mà ∠(CAE) =90^o⇒∠(HAC) +∠(EAN) =90^o(kề bù) (4)

Trong tam giác vuông AHC, ta có:

∠(AHC) =90^o⇒∠(HAC) +∠(HCA) =90^o (5)

Từ (4) và (5) suy ra: ∠(HCA) =∠(EAN) ̂

Xét hai tam giác vuông AHC và ENA, ta có:

∠(AHC) =∠(EAN) =90^o

AC = AE (gt)

∠(HCA) =∠(EAN)

Suy ra : ΔAHC= ΔENA(cạnh huyền, góc nhọn)

Vậy AH = EN (hai cạnh tương ứng)

Từ (3) và (6) suy ra: DM = EN

Vì DM ⇒AH và EN ⇒AH nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)

Gọi O là giao điểm của MN và DE

Xét hai tam giác vuông DMO và ENO, ta có:

∠(DMO) =∠(ENO) =90^o

DM= EN (gt)

∠(MDO) =∠(NEO)(so le trong)

Suy ra : ΔDMO= ΔENO(g.c.g)

⇒D = OE

Vậy MN đi qua trung điểm của DE

Bài 63 trang 146 sách bài tập Toán 7 Tập 1: Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC ở E, đường thẳng qua E và song song với AB cắt BC ở F. Chứng minh rằng:

a. AD = EF

b. ΔADE=Δ EFC

c. AE=EC

Lời giải:

a, Xét Δ DBFvà Δ FDE, ta có:

∠(BDF) =∠(DFE) (so le trong vì EF // AB)

DF cạnh chung

∠(DFB) =∠(FDE) (so le trong vì DE // BC)

Suy ra: Δ DBF=Δ FDE(g.c.g) ⇒ DB = EF (hai cạnh tương ứng)

Mà AD = DB (gt)

Vậy: AD = EF

b, Ta có: DE // BC (gt)

⇒∠(D₁ ) =∠B (đồng vị)

EF // AB (gt)

⇒∠(F₁ ) =∠B (đồng vị)

⇒∠(E₁ ) =∠A (đồng vị)

Xét Δ ADEvà Δ EFC, ta có:

∠(E₁ ) =∠A (chứng minh trên)

AD = EF

∠(F₁ ) =∠(D₁ ) (vì cùng bằng B)

Suy ra : Δ ADE= Δ EFC(g.c.g)

c,Vì : Δ ADE= Δ EFC nên AE = EC (hai cạnh tương ứng)

Bài 64 trang 146 sách bài tập Toán 7 Tập 1: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Vẽ điểm F sao cho E là trung điểm của DF. Chứng minh rằng:

a, DB = CF

b, Δ BDC= Δ FCD

c, DE//Bc và DE =1/2BC

Lời giải:

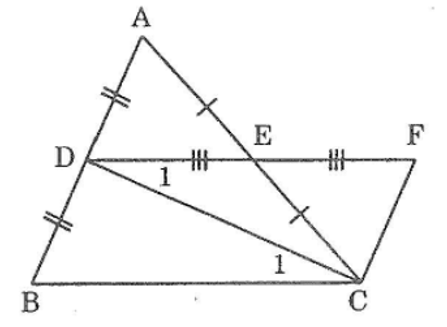
a, Xét ΔADE và ΔCFE, ta có:

AE = CE (gt)

∠(AED) =∠(CEF) (đối đỉnh)

DE=FE

Suy ra: ΔADE= ΔCFE (c.g.c)

⇒AD = CF (hai cạnh tương ứng)

Mà AD = DB (gt)

Vậy: DB = CF

b, Ta có: ΔADE= ΔCFE(chứng minh trên)

⇒∠(ADE) =∠(CFE) (hai góc tương ứng)

Suy ra: AD // CF (vì có cặp góc so le trong bằng nhau)

Hay AB // CF

Xét ΔBDC và ΔFCD, ta có:

BD = CF (chứng minh trên)

∠(BDC) =∠(FCD) (hai góc so le trong vì CF // AB)

DC cạnh chung

Suy ra: ΔBDC= ΔFCD (c.g.c)

c, Ta có: ΔBDC= ΔFCD(chứng minh trên)

Suy ra: ∠(C₁ ) =∠(D₁ ) (hai góc tương ứng)

Suy ra: DE // BC ( vì có hai góc so le trong bằng nhau)

ΔBDC= ΔFCD suy ra BC = DF (hai cạnh tương ứng)

Mà DE = 1/2 DF(gt). Vậy DE = 1/2 BC

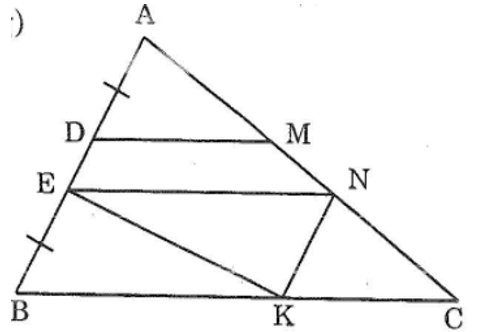
Bài 65 trang 146 sách bài tập Toán 7 Tập 1: Cho tam giác ABC. Trên cạnh AB lấy các điểm D và E sao cho AD = BE. Qua D và E, vẽ các đường thẳng song song với BC, chúng cắt AC theo thứ tự ở M và N. Chứng minh rằng DM + EN = NC

Hướng dẫn: qua N kẻ đường thẳng song song với AB

Lời giải:

Từ N kẻ đường thẳng song song vói AB cắt BC tại K. Nối EK.

Xét ΔBEK và Δ NKE, ta có:

∠(EKB) =∠(KEN) (so le trong vì EN // BC)

EK cạnh chung

∠(BEK) =∠(NKE) (so le trong vì EN // BC)

Suy ra: Δ BEK = Δ NKE(g.c.g)

Suy ra: BE = NK (hai cạnh tương ứng)

EN = BK (hai cạnh tương ứng)

Xét Δ ADM và Δ NKC, ta có:

∠A =∠(KNC) (đồng vị vì NK // AB)

AD = NK ( vì cùng bằng BE)

∠(ADM) =∠(NKC) (vì cùng bằng góc B)

Suy ra: Δ ADM = Δ NKC(g.c.g)

Suy ra: DM = KC (hai cạnh tương ứng)

Mà BC = BK + KC. Suy ra: BC = EN + DM

Bài 66 trang 146 sách bài tập Toán 7 Tập 1: Cho tam giác ABC có:∠ A =60^o

Các tia phân giác của các góc B, C cắt nhau ở I và cắt AC, AB theo thứ tự tại D, E. Chứng minh rằng: ID = IE

Hướng dẫn: kẻ tia phân giác góc BIC

Lời giải:

Trong ΔABC, ta có:

∠A +∠B +∠C =180^o (tổng ba góc trong tam giác)

⇒∠B +∠C =180-∠A =180-60=120^o

₁₂

∠(C₁ ) =∠(C₂ ) =1/2∠ C (gt)

Trong ΔBIC, ta có:

∠(BIC) =180^o(∠(B₁ ) +∠(C₁ ) )=180^o-(∠B /2+∠C /2)=180^o-60^o=120^o

Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K

Suy ra: ∠(I₂ ) =∠(I₃ ) =1/2 ∠(BIC) =60^o

Ta có: ∠(I₁ ) +∠(BIC) =180^o (hai góc kề bù)

⇒ ∠(I₁ ) =180^o-∠(BIC) =180^o-120^o=60^o

∠(I₄ ) =∠(I₁ ) =60^o(vì hai góc đối đỉnh)

Xét ΔBIE và ΔBIK, ta có

∠(B₂ ) =∠(B₁ ) (gt)

BI cạnhchung

∠(I₂ ) =∠(I₁ ) =60^o

Suy ra: ΔBIE= ΔBIK(g.c.g)

IK=IE (hai cạnh tương ứng) (1)

Xét ΔCIK và ΔCID, ta có

∠(C₂ ) =∠(C₁ ) (gt)

CI cạnh chung

∠(I₃ ) =∠(I₄ ) =60^o

Suy ra: ΔCIK= ΔCID(g.c.g)

IK=ID (hai cạnh tương ứng) (2)

Từ (1) và (2) suy ra: IE = ID

Bài 5.1 trang 146 sách bài tập Toán 7 Tập 1: Cho tam giác ABC và tam giác có 3 đỉnh là D,E,F. Biết AB= DF và ∠B=∠D

Trong các khẳng định sau,khẳng định nào đúng, khẳng định nào sai ?

a)Nếu ∠A = ∠F thì hai tam giác đó bằng nhau

b)Nếu ∠A = ∠E thì hai tam giác đó bằng nhau

c)Nếu ∠C = ∠E thì hai tam giác đó bằng nhau

Lời giải:

a) Đúng;

b) Sai;

c) Đúng.

Bài 5.2 trang 146 sách bài tập Toán 7 Tập 1: Cho tam giác ABC trên tia đối của tia AB lấy điểm D sao cho AD=AB.Trên tia đối của tia AC lấy điểm E sao cho AE=AC. Một đường thẳng đi qua A cắt DE và BC theo thứ tự tại M và N. Chứng minh rằng:

a)BC // DE

b)AM = AN

Lời giải:

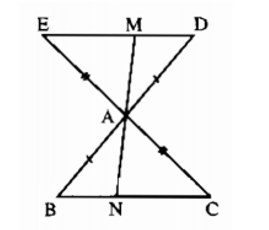
a) ΔABC = ΔADE (c.g.c)

nên ∠C = ∠E. Suy ra DE // BC.

b) ΔAEM = ΔACN (g.c.g) nên AM = AN.

Bài 5.3 trang 146 sách bài tập Toán 7 Tập 1: Chứng minh rằng nếu hai tam giác bằng nhau thì hai đường cao tương ứng bằng nhau

Lời giải:

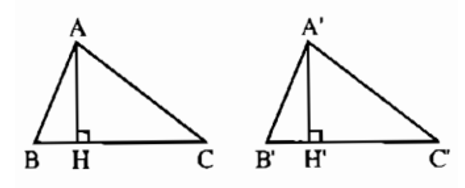
Xét các tam giác bằng nhau ΔABC = ΔA'B'C'. Kẻ AH ⊥ BC, A’H’ ⊥ B’C’

Suy ra ΔABC = ΔA'B'C' nên AC = A’C’, ∠C = ∠C'.

Suy ra ΔAHC = ΔA'H'C' (cạnh – huyền – góc nhọn) nên AH = A’H’.

Bài 5.4 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác giác ABC vuông tại A có AB = AC. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = AE. Đường thẳng đi qua D và vuông góc với BE cắt đường thẳng CA tại K. Chứng minh rằng AK = AC.

Lời giải:

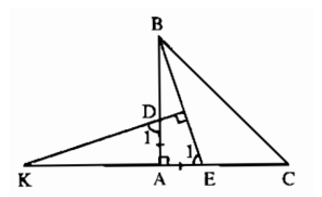
∠D = ∠E₁ (cùng phụ với ∠K)

Suy ra ΔKAD = ΔBAD (g.c.g), suy ra AK = AB.

Ta lại có AB = AC nên AK = AC.