Giải SBT Toán 7 Bài 6: Tam giác cân

Bài 67 trang 147 sách bài tập Toán 7 Tập 1: a, Tính góc ở đáy của một tam giác cân biết góc ở đỉnh bằng 50^o,bằng a^o.

b, Tính góc ở đỉnh của một tam giác cân biết góc ở đáy bằng 50^o,bằng a^o

Lời giải:

Vì tam giác cân có hai gốc ở đáy bằng nhau nên số đo của mỗi góc bằng 180^o trừ góc ở đỉnh rồi chia cho 2.

Vì tam giác cân có hai góc ở đáy bằng nhau nên góc ở đỉnh bằng 180^otrừ đi hai lần góc ở đáy.

Ta có: 180^o-50^o.2=180^o-100^o=80^o

180^o-a.2

Bài 68 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A có ∠A= 100°. Lấy điểm M thuộc cạnh AB, điểm N thuộc cạnh AC sao cho AM = AN. Chứng minh rằng MN // BC

Lời giải:

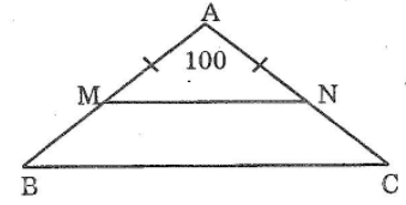
Mà AM = AN (gt) nên ∆AMN cân tại A =>∠AMN =∠ANM

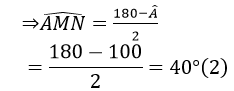
Từ (1) và (2) suy ra: ∠ B =∠AMN

Vậy MN // BC (vì có cặp góc ở vị trí đồng vị bằng nhau)

Bài 69 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB.

Chứng minh rằng BM = CN

Lời giải:

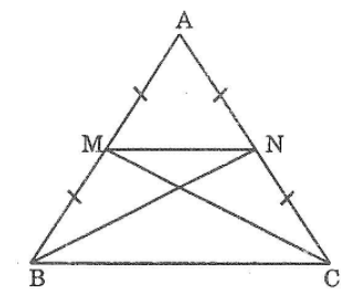
Xét ΔABM và ΔCAN, ta có:

AB = AC (gt)

∠A chung

AM=AN (cùng bằng một nửa AB, AC)

Suy ra: ΔABM = ΔCAN(c.g.c)

Vậy DM = CN ( hai cạnh tương ứng)

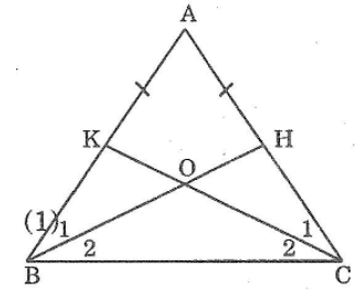
Bài 70 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH = AK. Gọi O là giao điểm của BH và CK.

Chứng minh rằng ΔOBClà tam giác cân.

Lời giải:

Xét ΔABH và ΔACK, ta có:

AB = AC (gt)

A chung

AH=AK (gt)

Suy ra: ΔABH= ΔACK(c.g.c)

⇒B₁ =C₁ (hai góc tương ứng)

∠ABC= B₁ +B₂9(2)

∠ACB=C₁+C₂ (3)

∠ABC=∠ACB (tính chất tam giác cân) (4)

Từ (1),(2),(3) và (4) suy ra: B₂=C₂hay &Delt;aBOC cân tại O

Bài 71 trang 147 sách bài tập Toán 7 Tập 1: Vẽ lại hình bên vào vở rồi đặt bài toán vẽ tam giác để có hình bên.

Lời giải:

- Vẽ tam giác ABC vuông tại A

- Vẽ tam giác đều ABD sao cho D và C nằm trên 2 nửa mặt phẳng đối nhau có bờ chứa đường thẳng AB.

- Vẽ tam giác vuông cân ADE sao cho E và B nằm trên 2 nửa mặt phẳng đối bờ chứa đường thẳng AD.

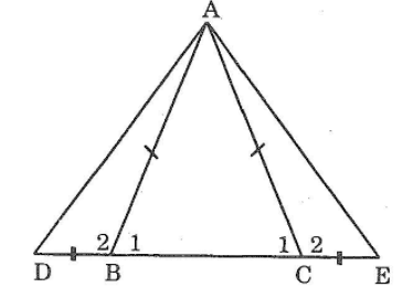
Bài 72 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh rằng ΔADE là tam giác cân.

Lời giải:

Ta có: ΔABC cân tại A

Suy ra:B₁=C₁ (tính chất tam giác cân)

Lại có:B₁ +B₂ =180^o (kề bù)

C₁ +C₁ =180^o (kề bù)

Suy ra: C₁ =B₁

Xét ΔABD và ΔACE, ta có:

AB = AC (gt)

C₁ =B₂ (chứng minh trên)

BD=CE (gt)

Suy ra: ΔABD=ΔACE(c.g.c)

⇒AD=AE ( hai cạnh tương ứng)

Vậy ΔADE cân tại A (theo định nghĩa tam giác cân)

Bài 73 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC. Tia phân giác của góc B cắt AC ở D. trên tia đối của tia BA lấy E sao cho BE = BC. Chứng minh rằng BD // EC

Lời giải:

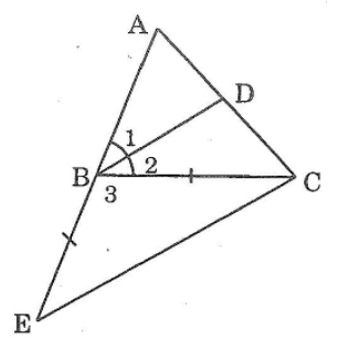
Ta có: BD là tia phân giác của ∠ABC (gt)

Suy ra:B₁=B₂= (1/2)ABC

Lại có: BE = BC (gt)

=>∆BEC cân tại B (theo định nghĩa)

∠E= ∠BCE (tính chất tam giác cân)

∆BEC có ABC là góc ngoài đỉnh B

=>∠ABC= ∠E + ∠BCE (tính chất góc ngoài tam giác)

Suy ra: ∠ABC=2∠E

Hay ∠E= ∠B₁= (1/2)∠ABC

Vậy BD // CE (vì có cặp góc ở vị trí đồng vị bằng nhau)

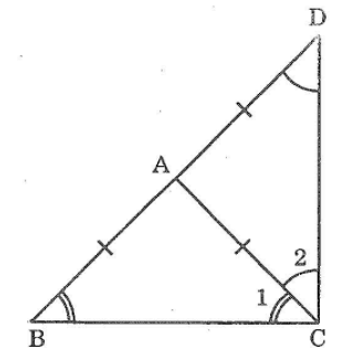
Bài 74 trang 147 sách bài tập Toán 7 Tập 1: Tính số đo các góc của tam giác ACD như hình bên.

Lời giải:

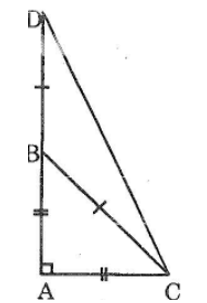
Ta có: ∆ABC vuông cân tại A

Suy ra: ∠ACB=∠ABC=45^o

Lại có: ∆BCD vuông cân tại B (BC = BD)

Suy ra: ∠BCD=∠Dtính chất tam giác cân)

Trong ∆BCD ta có ∠ABC góc ngoài tại đỉnh B

Do vậy: ∠ABC=∠BCD + ∠D (tính chất góc ngoài của tam giác)

Suy ra: ∠ABC= ∠2BCD

=>ACD=∠ACB + ∠BCD=45^o+22^o30'=67^o30'

Bài 75 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Tính số đo góc BCD

Lời giải:

Ta có: ∆ABC cân tại A

⇒B =C₁(tính chất tam giác cân)

Lại có: AD = AB (gt)

Suy ra: AD = AC do đó ∆ACD cân tại A

∠D =∠C₂(tính chất tam giác cân)

Mà ∠BCD =∠C₁+C₂̂

Nên ∠BCD =∠B +∠D(1)

Trong ∆BCD, ta có:

∠BCD +∠B +∠D =180^o (tổng 3 góc trong tam giác) (2)

từ (1)và (2)suy ra : 2 ∠BCD =180° hay∠BCD =90°

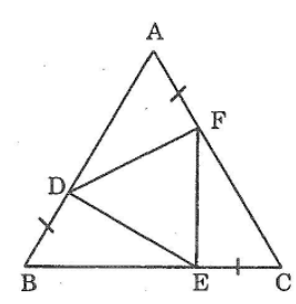
Bài 76 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A có cạnh bên bằng 3cm. Gọi D là một điểm thuộc đáy BC. Qua D, kẻ cac đường thẳng song song vói các cạnh bên, chúng cắt AB và AC theo thứ tự tại F và E.

Tính tổng DE + DF

Lời giải:

Ta có: DF // AC(gt)

=>D₁ =C (hai góc đồng vị) (1)

Lại có: ΔABC cân tại A

=>B =C (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra: B =D₁

Hay ΔBFD caab tại F =>BF = DF

Nối AD. Xét ΔAFD và ΔDEA có:

∠ADF =∠EAD(so le trong vì DF // AC)

AD cạnh chung

∠FDA =∠EDA(so le tronh vì DE // AB)

Suy ra: ΔAFD= ΔDEA(g.c.g)

AF = DF (hai cạnh tương ứng)

Vậy: DE_DF = AF + BF = AB = 3cm

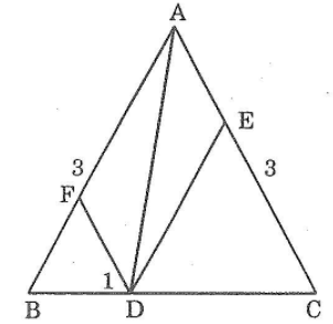
Bài 77 trang 148 sách bài tập Toán 7 Tập 1: Cho tam giác đều ABC. Lấy các điểm D, E , F theo thứ tựu thuộc các cạnh B. BC và cA sao cho AD = BE = CF. Chứng minh rằng tam giác DEF là tam giác đều?

Lời giải:

Ta có: AB = AD +DB (1)

BC = BE = EC (2)

AC = AF + FC (3)

AB = AC = BC (4)

AD = BE = CF (5)

Từ (1), (2), (3) và (4),(5) suy ra: BD = EC = AF

Xét ΔADF và ΔBED, ta có:

AD = BE (gt)

∠A =∠B =60^o (vì tam giác ABC đều)

AE=BD (chứng minh trên)

suy ra: ΔADF= ΔBED (c.g.c)

DF=ED (hai cạnh tương ứng) (6)

Xét ΔADF và ΔCFE, ta có:

AD = CF (gt)

∠A =∠C =60^o (vì tam giác ABC đều)

EC=AF (chứng minh trên)

suy ra: ΔADF= ΔCFE (c.g.c)

DF=FE (hai cạnh tương ứng) (7)

Từ (6) và (7) suy ra: DF – ED = FE

Vậy tam giác DFE đều

Bài 78 trang 148 sách bài tập Toán 7 Tập 1: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. qua I kẻ đường thẳng song song với BC. Gọi giao điểm của đường thẳng này với AB, AC theo thứ tự là D,E.

Chứng minh rằng: DE = BD + CE

Lời giải:

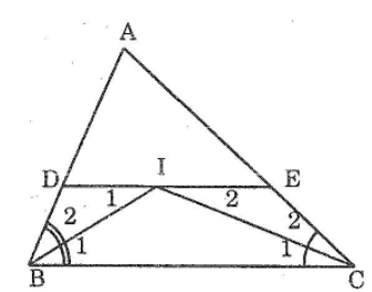
Ta có: DI // BC (gt)

Suy ra:∠I₁ =∠B₁(so le trong) (1)

Lại có:∠B₁ =∠B₂ (2)

(vì BI là yia phân giác góc B)

Từ (1) và (2) suy ra:∠I₁ =∠B₂

=>∆BDI cân tại D =>BD=DI (3)

Mà IE // BC (gt) =>∠I₁ =∠C₁ (so le trong) (4)

Đồng thời: ∠C₁=∠C₂ (vì CI là phân giác của góc C) (5)

Từ (4) và (5) suy ra: ∠C₁=∠C₂. Suy ra. ∠CEI cân tại E

Suy ra: CE = EI (hai cạnh tương ứng) (6)

Từ (3) và (6) suy ra: BD + CE = DI + EI = DE

Bài 79 trang 148 sách bài tập Toán 7 Tập 1: Cho đường tròn tâm O đường kính AB. Gọi M là điểm nằm trên đường tròn, tính số đo góc AMB.

Lời giải:

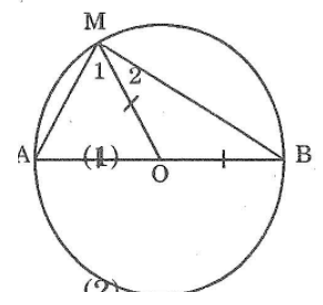
Nối OM, ta có:

OA = OM (bán kính đường tròn tâm O)

Nên ΔOAM cân tại O

⇒∠A =∠M₁(tính chất tam giác cân)(1)

OM = OB (bán kính đường tròn tâm O)

Suy ra: ΔOBM cân tại O

⇒∠B =∠M₂(tính chất tam giác cân) (2)

Trong ΔAMB ta có:

∠A =∠AMB =∠B =180 (tổng ba góc trong tam giác)

⇒∠A +∠B +∠M₁+∠M₂ =180 (3)

Từ (1), (2) và (3) suy ra: 2(M₁+M₂)=180^o

Vậy:

(∠M₁+∠M₂)=90^o hay (AMB) =90^o

Bài 80 trang 148 sách bài tập Toán 7 Tập 1: Đặt đề toán theo hình dưới đây. Sau đó vẽ lại hình theo đề toán rồi đo goác DAE

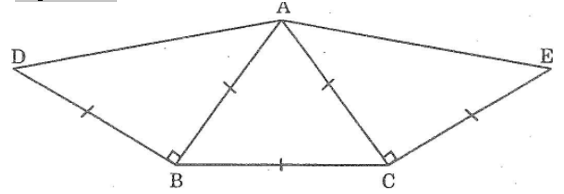
Lời giải:

Đề toán:

Vẽ tam giác ABC đều

Vẽ tam giác ABD vuông cân tại B sao cho D và C nằm trên hai nửa mặt phẳng bờ chứa đường thẳng AB.

Vẽ tam giác ACE vuông cân tại C sao cho E và B nằm trên hai nửa mặt phẳng đối có bờ chứa đường thẳng AC

Đo ∠DAE =150^o

Chứng minh:

∠DAE =∠DAB +∠BAC +∠CAE =45^o+60^o+45^o = 150^o

Bài 81 trang 148 sách bài tập Toán 7 Tập 1: Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình dưới ) là tam giác nhọn.

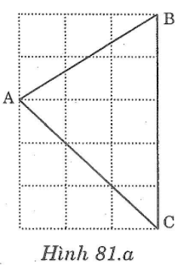
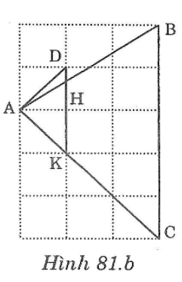
Lời giải:

Nối A với D tạo tành đường chéo ô vuông

Gọi K giao điểm AC với đỉnh ô vuông, H là giao điểm DK với đường kẻ ô vuông từ A.

Ta có: ΔAHK vuông cân tại H =>∠HAK =45^o

ΔAHD vuông cân tại H=>∠HAD =45^o

=>∠DAK =∠HAK +∠HAD =45^o+45^o=90^o

hay ∠DAC =90^o

=>∠BAC <90^o

Trên hình vẽ: ∠ACB <90^o và ∠ABC <90^o

Vậy tam giác ABC là tam giác nhọn

Bài 6.1 trang 148 sách bài tập Toán 7 Tập 1: Góc ADB trên hình bs 3 có số đo bằng

(A) 20^o;

(B) 25^o;

(C) 30^o;

(D) 35^o;

Hãy chọn phương án đúng.

Lời giải:

Chọn đáp án B

Bài 6.2 trang 148 sách bài tập Toán 7 Tập 1: Cho tam giác ABC vuông cân tại A. Trên tia đối của tia BC lấy điểm D sao cho BD = BA. Tính số đo góc ADB

Lời giải:

∠ADB = 22°30’.

Bài 6.3 trang 148 sách bài tập Toán 7 Tập 1: Cho tam giác ABC có ∠A= 100^o. Trên cạnh BC lấy điểm D và E sao cho BD = BA, CE = CA. Tính số do góc DAE.

Lời giải:

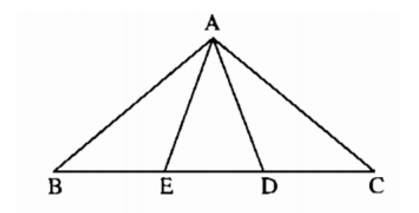
Tam giác cân ABC có ∠A = 100° nên ∠B = ∠C = 40°.

Ta tính được ∠ADB = 70°, ∠AEC = 70°.

Suy ra ∠DAE = 40°.

Bài 6.4 trang 148 sách bài tập Toán 7 Tập 1: Cho hình bs 4. Chứng minh rằng :

a) C,O,D thẳng hàng ;

b) BC = AD

Lời giải:

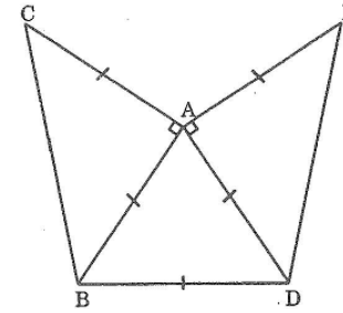
a) Các tam giác cân AOD, BOC có góc ở đáy bằng nhau nên góc ở đỉnh bằng nhau ∠AOD = ∠BOC. Ta lại có ∠AOD + ∠BOD = 180° nên ∠BOC + ∠BOD = 180°.

Vậy C, O, D thẳng hàng.

b) ΔBOC = ΔAOD (g.c.g), suy ra BC = AD.

Bài 6.5* trang 148 sách bài tập Toán 7 Tập 1: Cho tam giác ABC vuông tại A, ∠B = 30^o. Chứng minh rằng AC = (1/2)BC.

Lời giải:

Lấy điểm D trên cạnh BC sao cho ∠CAD = 60°. Tam giác ACD có ∠A₁ = 60°, ∠C = 60° nên là tam giác đều, suy ra AC = AD = DC.        (1)

Tam giác ABD có ∠A₂ = ∠B (cùng bằng 30°) nên là tam giác cân, suy ra AD = BD.        (2)

Từ (1) và (2) suy ra AC = DC = BD, tức là AC = 1/2BC.