Giải SBT Toán 7 Bài 8: Các trường hợp bằng nhau của tam giác vuông

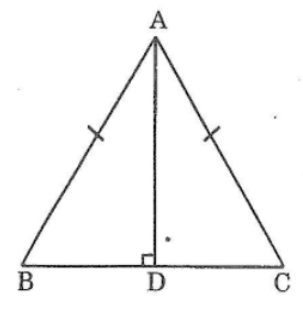
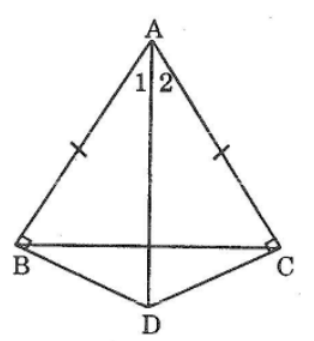
Bài 93 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác cân tại A. Kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A

Lời giải:

Xét hai tam giác vuông ADB và ADC, ta có:

∠(ADB) =∠(ADC) = 90^o

AB = AC (gt)

Ad cạnh chung

Suy ra: ΔADB= ΔADC(cạnh huyền, cạnh góc vuông)

⇒ ∠(BAD) =∠(CAD) (hai góc tương ứng)

Vậy ADI là tia phân giác ∠(BAC)

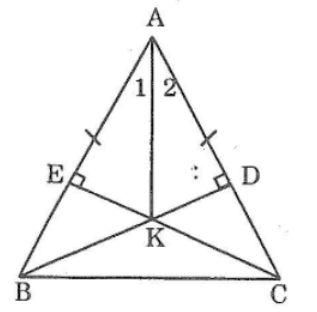
Bài 94 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Kẻ BD vuông góc với AC, kẻ CE vuông góc với AB. Gọi K là giao điểm của BD và CE. Chứng minh rằng Ak là tia phân giác của góc A.

Lời giải:

Xét hai tam giác vuông ADB và AEC, ta có:

∠(ADB) =∠(AEC) = 90^o

AB = AC (gt)

∠(DAB) =∠(EAC)

Suy ra: ΔADB= ΔAEC(cạnh huyền, cạnh góc vuông)

⇒AD=AE (hai cạnh tương ứng)

xét hai tam giác vuông ADK và AEK. Ta có:

∠(ADK) =∠(AEK) = 90^o

AD = AE (chứng minh trên)

AK cạnh chung

Suy ra: ΔADK= ΔAEK(cạnh huyền, cạnh góc vuông)

⇒∠(DAK) =∠(EAK) (hai góc tương ứng)

Vậy AK là tia phân giác của góc BAC

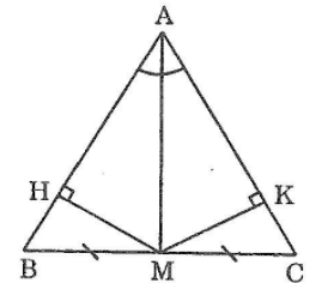
Bài 95 trang 151 sách bài tập Toán 7 Tập 1: Tam giác ABC có M là trung điểm BC,AM là tia phân giác góc A. Kẻ MH vuông góc với AB, MK vuông góc với AC. Chứng minh rằng:

a. MH = MK

b. ∠B =∠C

Lời giải:

Xét hai tam giác vuông AHM và AKM, ta có:

∠(AHM) =∠(AKM) =90^o

Cạnh huyền AM chung

∠(HAM) =∠(KAM) (gt)

⇒ ΔAHM= ΔAKM (cạnh huyền, góc nhọn)

Suy ra: MH = MK (hai cạnh tương ứng)

Xét hai tam giác vuông MHB và MKC, ta có:

∠(MHB) =∠(MKC) =90^o

MH = MK (chứng minh trên)

MC = MB (gt)

⇒ ΔMHB= ΔMKC (cạnh huyền, góc nhọn)

∠B =∠C (hai góc tương ứng)

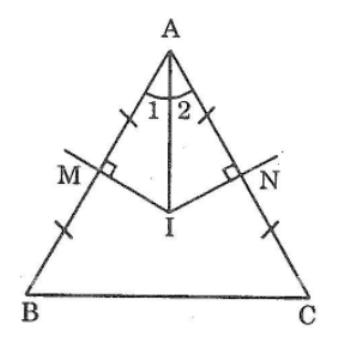
Bài 96 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Các đường trung trực của AB, AC cắt nhau ở I. chứng minh rằng AI là tia phân giác góc A.

Lời giải:

Ta có: AB = AC (gt) (1); AM = 1/2 AB (gt) (2);

AN = 1/2 AC (gt)(3)

Từ (1), (2) và (3) suy ra: AM = AN

Xét hai tam giác vuông AMI và ANI, ta có:

∠(AMI) =∠(ANI) =90^o

AM = AN (chứng minh trên)

AI cạnh huyền chung

⇒ ΔAMI= ΔANI (cạnh huyền, góc nhọn)

Suy ra: ∠(A₁ ) =∠(A₂) (hai góc tương ứng)

Vậy AI là tia phân giác của ∠(BAC)

Bài 97 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Qua B kẻ đường thẳng vuông góc với AB, qua C kẻ đường thẳng vuông góc với AC, chứng cắt nhau tại D. chứng minh rằng AD là tia phân giác của góc A.

Lời giải:

Xét hai tam giác vuông ABD và ACD, ta có:

∠(ABD) =∠(ACD) =90^o

Cạnh huyền AD chung

AB = AC

⇒ ΔABD= ΔACD (cạnh huyền, góc nhọn)

Suy ra: ∠(A₁ ) =∠(A₂) (hai góc tương ứng)

Suy ra AD là tia phân giác góc A

Bài 98 trang 151 sách bài tập Toán 7 Tập 1: Tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A. Chứng minh rằng tam giác ABC là tam giác cân.

Lời giải:

Kẻ MH ⊥ AB, MK ⊥AC

Xét hai tam giác vuông AHM và AKM, ta có:

∠(AHM) =∠(AKM) =90^o

Cạnh huyền AM chung

∠(HAM) =∠KAM) (gt)

⇒ ΔABD= ΔACD (cạnh huyền, góc nhọn)

Suy ra: MH = MK (hai cạnh tương ứng)

Xét hai tam giác vuông MHB và MKC, ta có:

∠(MHB) =∠(MKC) =90^o

MB=MC

MH=MK

⇒ ΔMHB= ΔMKC (cạnh huyền, góc nhọn)

Suy ra: ∠B =∠C (hai góc tương ứng)

Vậy tam giác ABC cân tại A

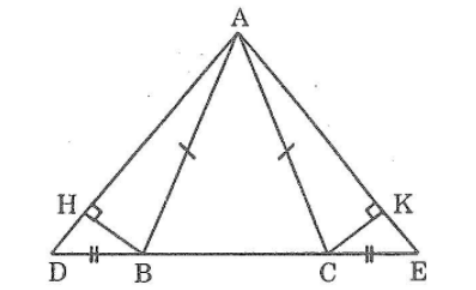
Bài 99 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Trên tia đối của tai BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông với AD, kẻ CK vuông góc với AE. Chứng minh rằng:

BH = CK

ΔABH= ΔACK

Lời giải:

Vì ΔABC cân tại A nên∠(ABC) =∠(ACB) (tính chất tam giác cân)

Ta có: ∠(ABC) +∠(ABD) =180^o(hai góc kề bù)

∠(ACB) +∠(ACE) =180^o(hai góc kề bù)

Suy ra: ∠(ABD) =∠(ACE)

Xét ΔABD và ΔACE, ta có:

AB = AC (gt)

∠(ABD) =∠(ACE) (chứng minh trên)

BD=CE (gt)

Suy ra: ΔABD= ΔACE (c.g.c)

⇒∠D =∠E (hai góc tương ứng)

Xét hai tam giác vuông ΔBHD và ΔCKE, ta có:

∠(BHD) =∠(CKE)

BD=CE (gt)

∠D =∠E (chứng minh trên)

Suy ra: ΔBHD= ΔCKE (c.g.c)

Suy ra: BH = CK (hai cạnh tương ứng)

Xét ΔAHB và ΔACK, ta có:

AB = AC (gt)

∠(ABD) =∠(ACE) =90^o

BH=CK

Suy ra: ΔABH= ΔACK (cạnh huyền, góc nhọn)

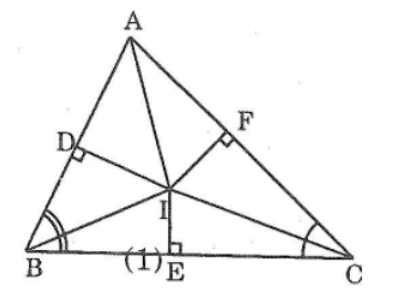
Bài 100 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác ABC. Các tia phân giác của các góc B và C cát nhau tại I. chứng minh rằng AI là tia phân giác của góc A.

Hướng dẫn: từ I, kẻ các đường vuông góc với các cạnh của tam giác ABC.

Lời giải:

Kẻ: ID⊥AB, IE⊥BC, IF⊥AC

Xét hai tam giác vuông ΔIBD và ΔIEB, ta có:

∠(DBI) =∠(EBI) (gt)

∠(IDB) =∠(IEB) =90^o

BI cạnh chung

Suy ra: ΔIDB= ΔIEB(cạnh huyền, góc nhọn)

Suy ra: ID = IE ( hai cạnh tương ứng)

Xét hai tam giác vuông ΔIEC và ΔIFC, ta có:

∠(ECI) =∠(FCI)

∠(IEC) =∠(IFC) =90^o

CI cạnh huyền chung

Suy ra: ΔIEC= ΔIFC(cạnh huyền góc nhọn)

Suy ra: IE = IF (hai cạnh tương ứng) (2)

Từ (1) và (2) suy ra: ID = IF

Xét hai tam giác vuông ΔIDA và ΔIFA, ta có:

ID=IF

∠(IDA) =∠(IFA) =90^o

AI cạnh huyền chung

Suy ra: ΔIDA= ΔIFA(cạnh huyền.cạnh góc vuông)

Suy ra: ∠(DAI) =∠(FAI) (hai góc tương ứng)

Vậy AI là tia phân giác góc A

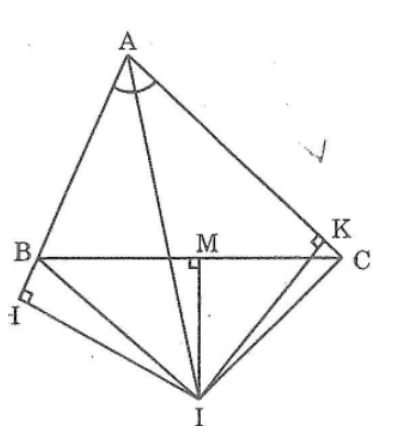
Bài 101 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác AB < AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. kẻ IH vuông góc với đường thẳng AB, kẻ IK vuông góc với đường thẳng AC. Chứng minh rằng BH = CK.

Lời giải:

Xét ΔBMI và ΔCMI, ta có:

∠(BMI) =∠(CMI) =90^o (gt)

BM=CM

MI cạnh chung

Suy ra: ΔBMI= ΔCMI(c.g.c)

Suy ra: IB = IC ( hai cạnh tương ứng)

Xét hai tam giác vuông ΔIHA và ΔIKA, ta có:

∠(HAI) =∠(KAI)

∠(IHA) =∠(IKA) =90^o

AI cạnh huyền chung

Suy ra: ΔIHA= ΔIKA(cạnh huyền góc nhọn)

Suy ra: IH= IK (hai cạnh tương ứng)

Xét hai tam giác vuông ΔIHB và ΔIKC, ta có:

IB=IC

∠(IHB) =∠(IKC) =90^o

IH=IK (chứng minh trên)

Suy ra: ΔIHB= ΔIKC(cạnh huyền.cạnh góc vuông)

Suy ra: BH=CK(hai cạnh tương ứng)

Bài 8.1 trang 152 sách bài tập Toán 7 Tập 1: Trong các khẳng định sau, khẳng định nào là đúng, khẳng định nào là sai ?

Các tam giác vuông ABC và DEF có ∠A=∠D=90^o, AC=DE bằng nhau nếu có thêm :

a) BC = EF;

b) ∠C = ∠E;

c) ∠C = ∠F;

Lời giải:

a) Đúng;

b) Đúng;

c) Sai.

Bài 8.2 trang 152 sách bài tập Toán 7 Tập 1: Các tam giác vuông ABC và DEF có ∠A = ∠D = 90^o,AC = DF,∠B = ∠E.Các tam giác vuông có bằng nhau không

Lời giải:

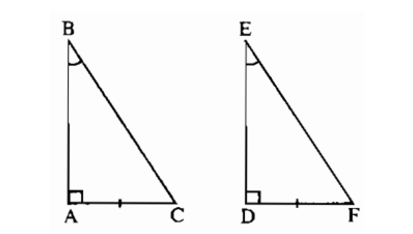
∠B = ∠E nên ∠C = ∠F.

Ta có ΔABC = ΔDEF (g.c.g).

Bài 8.3 trang 152 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Trên tia đối BC lấy điểm D, Trên tia đối của tia CB lấy điểm E sao cho ∠BAD = ∠CAE. Kẻ BH vuông góc với AD (H ∈ AD). kẻ CK vuông góc với AE (K ∈ AE). Chứng minh rằng :

a) BD = CE

b) BH = CK

Lời giải:

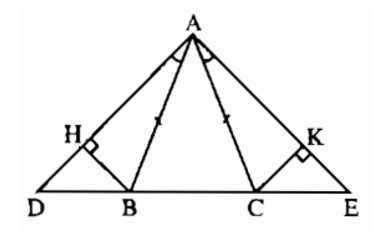
a) ΔABD = ΔACE (g.c.g) suy ra BD = CE.

b) ΔBHD = ΔCKE (cạnh huyền – góc nhọn), suy ra BH = CK.