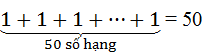Giải SBT Toán 7 Bài 7: Đa thức một biến

Bài 34 trang 24 sách bài tập Toán 7 Tập 2: Cho ví dụ một đa thức một biến mà:

a. Có hệ số cao nhất bằng 10, hệ số tự do bằng -1

b. Chỉ có ba hạng tử

Lời giải:

Có nhiều đáp số, chẳng hạn:

a) 10x⁵ + x – 1;       10x⁵ - x³ + x² – 1

b) 4x⁵ - x⁴ + 2x³;       x⁵ - x² + x.

Bài 35 trang 24 sách bài tập Toán 7 Tập 2: Thu gọn các đa thức sau và sắp xếp theo lũy thừa giảm của biến:

a. x⁵ – 3x² + x⁴ - 1/2 x – x⁵ + 5x⁴ + x² – 1

b. x – x⁹ + x² – 5x³ + x⁶ – x + 3x⁹ + 2x⁶ – x³ + 7

Lời giải:

a. Ta có: x⁵ – 3x² + x⁴ - 1/2 x – x⁵ + 5x⁴ + x² – 1 = -2x² + 6x⁴ - 1/2 x – 1

Sắp xếp: 6x⁴ – 2x² - 1/2 x - 1

b. Ta có: x – x⁹ + x² – 5x³ + x⁶ – x + 3x⁹ + 2x⁶ – x³ + 7

= 2x⁹ + x² – 6x³ + 3x⁶ + 7

Sắp xếp: 2x⁹ + 3x⁶ – 6x³ + x² + 7

Bài 36 trang 24 sách bài tập Toán 7 Tập 2: Thu gọn và sắp xếp các số hạng của đa thức theo lũy thừa tăng của biến. Tìm hệ số cao nhất, hệ số tự do:

a. x⁷ – x⁴ + 2x³ – 3x⁴ – x² + x⁷ – x + 5 – x³

b. 2x² – 3x⁴ – 4x⁵ - 1/2 x – x² + 1

Lời giải:

a. Ta có: x⁷ – x⁴ + 2x³ – 3x⁴ – x² + x⁷ – x + 5 – x³

= 2x⁷ – 4x⁴ + x³ – x + 5 – x²

Sắp xếp: 5 – x – x² + x³ – 4x⁴ + 2x⁷

b. Ta có: 2x² – 3x⁴ – 4x⁵ - 1/2 x – x² + 1 = -2x² – 3x⁴ – 4x⁵ - 1/2 x + 1

Sắp xếp: 1 - 1/2 x – 2x² – 3x⁴ – 4x⁵

Hệ số cao nhất là -4, hệ số tự do là 1.

Bài 37 trang 25 sách bài tập Toán 7 Tập 2: Tính giá trị của các đa thức sau:

a. x² + x⁴ + x⁶ + x⁸ + … + x¹⁰⁰ tại x = -1

b. ax² + bx + c tại x = -1; x = 1 (a, b, c là hằng số)

Lời giải:

a. Thay x = -1 và đa thức, ta có:

(-1)² + (-1)⁴ + (-1)⁶ + … + (-1)¹⁰⁰ =

Vậy giá trị đa thức bằng 50 tại x = -1.

b. * Thay giá trị x = -1 vào đa thức, ta có:

a(-1)² + b(-1) + c = a – b + c

Vậy giá trị đa thức bằng a – b + c tại x = -1

* Thay giá trị x = 1 vào đa thức, ta có:

a.1² + b.1 + c = a + b + c

Vậy giá trị đa thức bằng a + b + c tại x = 1.

Bài 7.1 trang 25 sách bài tập Toán 7 Tập 2: Cho f(x)= x⁵ + 3x² − 5x³ − x⁷ + x³ + 2x² + x⁵ − 4x² − x⁷;

g(x) = x⁴ + 4x³ − 5x⁸ − x⁷ + x³ + x² − 2x⁷ + x⁴ – 4x² − x⁸.

Thu gọn và sắp xếp các đa thức f(x) và g(x) theo luỹ thừa giảm của biến rồi tìm bậc của đa thức đó.

Lời giải:

f(x) = x⁵ + 3x² − 5x³ − x⁷ + x³ + 2x² + x⁵ − 4x² − x⁷

⇒ f(x) =2x⁵ - 4x³ + x²

Đa thức có bậc là 5

g(x) = x⁴ + 4x³ – 5x⁸ – x⁷ + x³ + x² – 2x⁷ + x⁴ – 4x² – x⁸

⇒ g(x) = -6x⁸ - 3x⁷ + 2x⁴ + 5x³ - 3x².

Đa thức có bậc là 8.

Bài 7.2 trang 25 sách bài tập Toán 7 Tập 2: Giá trị của đa thức x + x³ + x⁵ + x⁷ + x⁹ + ...... + x¹⁰¹ tại x = -1 là:

(A) -101;

(B) -100;

(C) -51;

(D) -50

Hãy chọn phương án đúng.

Lời giải:

Chọn đáp án C