Giải SBT Toán 7 Bài 8: Cộng, trừ đa thức một biến

Bài 38 trang 25 sách bài tập Toán 7 Tập 2: Tính f(x) + g(x) với:

f(x) = x⁵ – 3x² + x³ – x² – 2x + 5

g(x) = x² – 3x + 1 + x² – x⁴ + x⁵

Lời giải:

Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:

* Ta có: f(x) = x⁵ – 3x² + x³ – x² – 2x + 5 = x⁵ + x³ – 4x² – 2x + 5

g(x) = x² – 3x + 1 + x² – x⁴ + x⁵ = x⁵ – x⁴ + 2x² – 3x + 1

* f(x) + g(x):

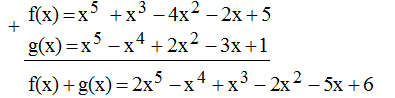
Bài 39 trang 25 sách bài tập Toán 7 Tập 2: Tính f(x) – g(x) với:

f(x) = x⁷ – 3x² – x⁵ + x⁴ – x² + 2x – 7

g(x) = x – 2x² + x⁴ – x⁵ – x⁷ – 4x² – 1

Lời giải:

Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:

* Ta có: f(x) = x⁷ – 3x² – x⁵ + x⁴ – x² + 2x – 7

            = x⁷ – x⁵ + x⁴ – 4x² + 2x - 7

g(x) = x – 2x² + x⁴ – x⁵ – x⁷ – 4x² – 1

            = -x⁷ – x⁵ + x⁴ – 6x² + x – 1

* f(x) – g(x)

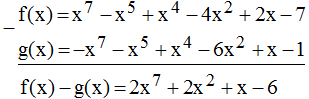
Bài 40 trang 25 sách bài tập Toán 7 Tập 2: Cho các đa thức:

            f(x) = x⁴ – 3x² + x – 1

            g(x) = x⁴ – x³ + x² + 5

a. Tìm h(x) biết f(x) + h(x) = g(x)

b. Tìm h(x) biết f(x) – h(x) = g(x)

Lời giải:

a. Ta có: f(x) + h(x) = g(x)

Suy ra: h(x) = g(x) – f(x) = (x⁴ – x³ + x² + 5) – (x⁴ – 3x² + x – 1)

            = x⁴ – x³ + x² + 5 – x⁴ + 3x² – x + 1

            = -x³ + 4x² – x + 6

b. Ta có: f(x) – h(x) = g(x)

Suy ra: h(x) = f(x) – g(x) = (x⁴ – 3x² + x – 1) – (x⁴ – x³ + x² + 5)

            = x⁴ – 3x² + x – 1 – x⁴ + x³ – x² – 5

            = x³ – 4x² + x – 6

Bài 41 trang 26 sách bài tập Toán 7 Tập 2: Cho các đa thức:

f(x) = a_nXⁿ + a_n – 1X^{n– 1} + … + a₁x + a_o

g(x) = b_nXⁿ + b_{n – 1}X^{n– 1} + … + b₁x + b_o

a. Tính f(x) + g(x)

b. Tính f(x) – g(x)

Lời giải:

a.

   f(x) = a_nXⁿ + a_n – 1X^{n– 1} + … + a₁x + a_o

+

   g(x) = b_nXⁿ + b_{n – 1}X^{n– 1} + … + b₁x + b_o

--------------------------------------------------------

f(x) + g(x) = (a_n + b_n)Xⁿ + (a_n – 1 + b_{n – 1})X^{n– 1} + ….. + (a₁ + b₁)x + (a_o + b_o)

b.

   f(x) = a_nXⁿ + a_n – 1X^{n– 1} + … + a₁x + a_o

-

   g(x) = b_nXⁿ + b_{n – 1}X^{n– 1} + … + b₁x + b_o

--------------------------------------------------------

f(x) - g(x) = (a_n - b_n)Xⁿ + (a_{n– 1} - b_{n – 1})X^{n– 1} + ..… + (a₁ - b₁)x + (a_o - b_o)

Bài 42 trang 26 sách bài tập Toán 7 Tập 2: Tính f(x) + g(x) – h(x) biết:

f(x) = x⁵ – 4x³ + x² – 2x + 1

g(x) = x⁵ – 2x⁴ + x² – 5x + 3

h(x) = x⁴ – 3x² + 2x – 5

Lời giải:

Ta có: f(x) = x⁵ – 4x³ + x² – 2x + 1

      g(x) = x⁵ – 2x⁴ + x² – 5x + 3

      h(x) = x⁴ – 3x² + 2x – 5

Suy ra: f(x) + g(x) – h(x)

      = (x⁵ – 4x³ + x² – 2x + 1) + (x⁵ – 2x⁴ + x² – 5x + 3) – (x⁴ – 3x² + 2x – 5)

      = x⁵ – 4x³ + x² – 2x + 1 + x⁵ – 2x⁴ + x² – 5x + 3 – x⁴ + 3x² - 2x + 5

      = (1 + 1)x⁵ – (2 + 1)x⁴ – 4x³ + (1 + 1 + 3)x² - (2 + 5 + 2)x + (1 + 3 + 5)

      = 2x⁵ – 3x⁴ – 4x³ + 5x² – 9x + 9

Bài 8.1 trang 26 sách bài tập Toán 7 Tập 2: Cho

f(x) = x² + 2x³− 7x⁵ − 9 − 6x⁷ + x³ + x² + x⁵ − 4x² + 3x⁷;

g(x) = x⁵ + 2x³ − 5x⁸ − x⁷ + x³ + 4x² -5x⁷ + x⁴ − 4x² − x⁶ – 12;

h(x) = x + 4x⁵ − 5x⁶ − x⁷ + 4x³ + x² − 2x⁷ + x⁶ − 4x² − 7x⁷ + x.

a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa tăng của biến.

b) Tính f (x) + g (x) – h (x)

Lời giải:

a) f(x) = −9 − 2x²+3x³ − 6x⁵ − 3x⁷

g(x) = −12 + 3x³ + x⁴ + x⁵ − 6x⁷− 5x⁸

h(x) = 2x − 3x² + 4x³ + 4x⁵ − 4x⁶ − 10x⁷

b) f(x) + g(x) − h(x) = −21 − 2x + x² + 2x³ + x⁴ − 9x⁵ + 3x⁶ + x⁷ − 5x⁸.

Bài 8.2 trang 26 sách bài tập Toán 7 Tập 2: Thu gọn đa thức (4x³ + 2x² − 1) − (4x³ − x² + 1) ta được:

(A) x²

(B) x² − 2

(C) 3x² - 2

(D)8x³ + x²

Hãy chọn phương án đúng.

Lời giải:

Chọn đáp án C